 |
|
Quadratische Funktionen (Parabel) der Funktionsklassen |


Die quadratische Funktion (Parabel)
 Den angeführten Definitions-begriff einer Funktion verdeutlicht die nebenstehende Graphik. Den angeführten Definitions-begriff einer Funktion verdeutlicht die nebenstehende Graphik.Jedem einzelnen x ist durch die Funktionsvorschrift y=ax2+bx+c genau ein und nur ein y-Wert zugeordnet. |
Auffrischung Mittelstufenwissen
| Die allgemeinen Form einer quadratischen Funktionsgleichung lautet: |
| f(x)=ax2+bx+c. |
| Die Variablen a, b und c haben dabei die nachfolgend näher beschriebene Bedeutung: |
Bedeutung des Parameters a
Der Parameter 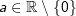 bestimmt die Öffnung (Streckung bzw. Stauchung in y-Richtung) der Parabel. Es gilt: bestimmt die Öffnung (Streckung bzw. Stauchung in y-Richtung) der Parabel. Es gilt: |
||
| Wert von a | Auswirkung | Grafik |
| a > 1 | Nach oben geöffnete, gestreckte Parabel |  |
| a = 1 | Nach oben geöffnete Normalparabel |  |
| a < 1 | Nach oben geöffnete, gestauchte Parabel |  |
| -1 < a < 0 | Nach unten geöffnete, gestauchte Parabel |  |
| a = -1 | Nach unten geöffnete Normalparabel |  |
| a < -1 | Nach unten geöffnete, gestreckte Parabel |  |
Bedeutung des Parameters b
Der Parameter 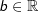 bestimmt eine Verschiebung der Parabel in x-Richtung. bestimmt eine Verschiebung der Parabel in x-Richtung.Zur Feststellung der Verschiebungsweite muss die allgemeine Funktionsgleichung f(x)= ax²+bx+c in die Scheitelpunktgleichung f(x)=a(x-xs )2+ys überführt werden, wobei xs und ys die Koordinaten des Scheitelpunkts S(xs|ys) sind. Die Gleichungsumstellung erfolgt über die quadratische Ergänzung mit |
||
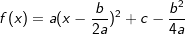 . . |
||
Mit  und und 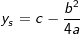 kann der Scheitel jedoch jederzeit auch ohne Formelumstellung ermittelt werden. kann der Scheitel jedoch jederzeit auch ohne Formelumstellung ermittelt werden. |
||
| Wert von xs | Auswirkung | Grafik |
| xs > 0 | Die Parabel ist in x-Richtung nach rechts verschoben. |  |
| xs = 0 | Die Parabel ist in x-Richtung nicht verschoben. |  |
| xs < 0 | Die Parabel ist in x-Richtung nach links verschoben. |  |
Bedeutung des Parameters c
Der Parameter 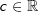 bestimmt die Verschiebung der Parabel in y-Richtung. Es gilt: bestimmt die Verschiebung der Parabel in y-Richtung. Es gilt: |
||
| Wert von c | Auswirkung | Grafik |
| c > 0 | Die Parabel ist in y-Richtung nach oben verschoben. |  |
| c = 0 | Die Parabel ist in y-Richtung nicht verschoben. |  |
| c < 0 | Die Parabel ist in y-Richtung nach unten verschoben. | 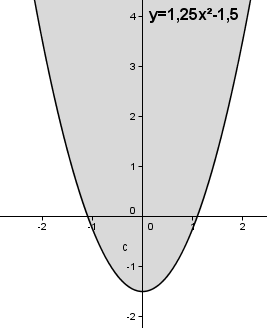 |
Beispiele
Beispiel 1Lösung 1 |
Beispiel 2Lösung 2aLösung 2bLösung 2c |
Beispiel 3Lösung 3aLösung 3bLösung 3c |
Erweitertes Wissen quadratische Funktionen
| Zum erweiterten Wissen über die quadratischen Funktionen gehören die Themenkreise • Scheitelform; • Symmetrie- und Globalverhalten; • Schnittpunkte mit den Koordinatenachsen; • Schnittpunkte zweier Parabeln; • Aufstellung von Funktionsgleichungen; • Anwendungsorientierte Themen; • Quadratische Funktionen mit Parameter. Nachfolgend werden die einzelnen Themenkreise behandelt. |
Scheitelform
| Eine quadratische Funktionsgleichung hat – je nachdem ob sie nach oben oder nach unten geöffnet ist – einen tiefsten bzw. einen höchsten Punkt. Diesen Punkt nennen wir den Scheitelpunkt (Scheitel) einer Parabel. Die Funktionsgleichung einer Parabel kann auch über die Scheitelform dargestellt werden mit |
| f(x)=a(x-xS)2+yS |
| mit a als Streckungsfaktor in y-Richtung und S(xs |ys) dem Scheitelpunkt und seinen Koordinaten xs und ys. Dabei kann die Hauptform f(x)=ax2+bx+c jederzeit aus der Scheitelform hergeleitet werden durch Auflösung der binomischen Formel (x-xs )2. Auf die Auflösung binomischer Formeln wird hier nicht mehr näher eingegangen, siehe hierzu den Portalteil „Binomische Formeln“. Umgekehrt kann die Scheitelform jederzeit aus der Hauptform hergeleitet werden. Hierzu bedienen wir uns der quadratischen Ergänzung, deren Herleitung kurz wiederholt werden soll. Ausführliche Erläuterungen hierzu findest du ebenfalls im Portalteil „Binomische Formeln“. |
Herleitung der Scheitelform aus der Hauptform
Symmetrie- und Globalverhalten
Es gibt zwei Arten von Symmetrieverhalten, nämlich die Achsensymmetrie und die Punktsymmetrie. Genaueres hierüber erfährst du um Kapitel „Graphen und Funktionen analysieren“.  Eine quadratische Funktion ist stets achsensymmetrisch zur Achse, die durch den Scheitelpunkt verläuft. Eine quadratische Funktion ist stets achsensymmetrisch zur Achse, die durch den Scheitelpunkt verläuft.Beim Globalverhalten will man wissen, wo der Graph einer Funktion herkommt und wo er hinläuft. Will man wissen, wo der Graph einer Funktion herkommt, muss man den y-Wert der Funktion für den Wert x=-∞ bestimmen. Will man wissen, wo der Graph einer Funktion hinläuft, muss man den y-Wert der Funktion für den Wert x=+∞ bestimmen. Der Graph einer quadratischen Funktion kommt aus dem II. Quadranten und verläuft in den I. Quadranten, sofern die Parabel nach oben geöffnet ist. Der Graph einer quadratischen Funktion kommt aus dem III. Quadranten und verläuft in den IV. Quadranten, sofern die Parabel nach unten geöffnet ist. Beispiel 5Lösung 5 |
Schnittpunkte mit den Koordinatenachsen
 Es gibt zwei Arten von Schnittpunkten mit den Koordinatenachsen. Es gibt zwei Arten von Schnittpunkten mit den Koordinatenachsen.Die erste Art sind die Schnittpunkte mit der x-Achse, Nullstellen genannt. Eine Nullstelle heißt Nullstelle, weil dort der y-Wert Null ist. Aus dieser Tatsache heraus lassen sich Nullstellen berechnen, indem man den y-Wert der Funktionsgleichung auf den Wert null setzt und die Gleichung nach x auflöst. Die zweite Art ist der Schnittpunkt mit der y-Achse, vielfach auch als y-Achsenabschnitt bezeichnet. Im Schnittpunkt mit der y-Achse ist der x-Wert Null. Aus dieser Tatsache heraus lässt sich Schnittpunkt mit der y-Achse berechnen, indem man alle Vorkommen von x auf null setzt und y berechnet, also f(0) bildet. |
Beispiel 6Lösung 6 |
Beispiel 7Lösung 7 |
Beispiel 8Lösung 8 |
Merksatz Schnittpunkte mit den Koordinatenachsen
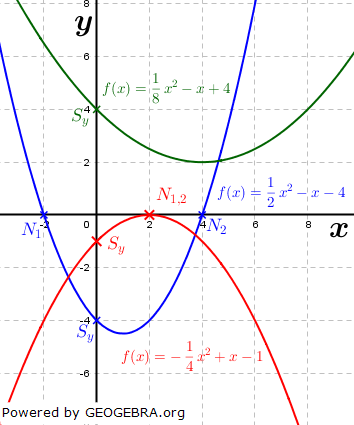 Die Schnittpunkte einer Funktion f mit der x-Achse heißen Nullstellen. Die Schnittpunkte einer Funktion f mit der x-Achse heißen Nullstellen.Wir berechnen Nullstellen, indem wir die Funktionsgleichung f(x) auf null setzen und nach x auflösen. Hat die auf null gesetzte Funktionsgleichung keine Lösung, so existieren auch keine Nullstellen. Die Schnittpunkte einer Funktion f mit der y-Achse wird auch als y-Achsenabschnitt bezeichnet. Wir berechnen den Schnittpunkt mit der y-Achse, indem wir f(0) bilden. |
Gegenseitige Lage Parabel und Gerade
| Eine Parabel und eine Gerade können verschiedene Lagen zueinander haben. Zur Untersuchung dieser gegenseitigen Lage prüfen wir, ob es gemeinsame Punkte gibt. Wir erinnern uns an einen Basissatz der Funktionsbetrachtung: | ||
|
||
Beispiel 9Lösung 9 |
||
Beispiel 10Lösung 10 |
||
Beispiel 11Lösung 11 |
Merksatz Lage von Gerade und Parabel
| Schneidet eine Gerade eine Parabel in zwei verschiedenen Punkten, so heißt diese Gerade Sekante; die beiden Punkte nennen wir Schnittpunkte. Berührt eine Gerade eine Parabel in einem Punkt, so heißt diese Gerade Tangente, den gemeinsamen Punkt nennen wir Berührpunkt. Haben eine Gerade und eine Parabel keinen gemeinsamen Punkte, so heißt diese Gerade Passante. |
Aufstellung von Funktionsgleichungen
 Durch welche Parabel kann der Verlauf des Brückenbogens der Yangtze River Brücke (China) näherungsweise beschrieben werden? Durch welche Parabel kann der Verlauf des Brückenbogens der Yangtze River Brücke (China) näherungsweise beschrieben werden?In vielen Fällen ist der Term einer quadratischen Funktion nicht von vornherein bekannt. Ausgehend von bestimmten Eigenschaften eines parabelförmigen Gebildes, können wir jedoch einen solchen Term bestimmen. Im obigen Bild z. B. wäre der höchste Punkt des Brückenbogens von Interesse, denn den könnten wir zum Scheitelpunkt einer Parabel erklären. Weiterhin könnten wir die linke und rechte Verankerung des Bogens am Ufer als Nullstellen einer Parabel in einem geeigneten Koordinatensystem ansehen. Alleine aus diesen beiden Eigenschaften ließe sich dann ein quadratischer Funktionsterm aufstellen.
|
|||||||||||||||||||||||
| Wollen wir nun einen Funktionsterm bestimmen, so kommt es darauf an, was gegeben ist. Ist der Scheitel bekannt, wird man den Funktionsterm in der Scheitelform ansetzen. Sind zwei Nullstellen bekannt, wählen wir die Produktform. Die Hauptform hat drei Unbekannte a, b, und c, dazu benötigen wir drei bekannte Punkte, die auf der Parabel liegen. Die genaue Vorgehensweise kannst du in den nächsten vier Beispielen sehen. |
|||||||||||||||||||||||
Beispiel 12Lösung 12aLösung 12bLösung 12c |
|||||||||||||||||||||||
Beispiel 13Lösung 13 |
|||||||||||||||||||||||
Beispiel 14Lösung 14 |
|||||||||||||||||||||||
Beispiel 15Lösung 15 |
|||||||||||||||||||||||
Quadratische Funktionen der Anwendungsorientierung
| Viele Realsituationen unserer Umwelt lassen sich durch Parabelfunktionen beschreiben. Mit ihrer Hilfe kann man z. Bsp. den Verlauf eines Brückenbogens beschreiben. Eine große Anzahl von Naturgesetzen kann durch Parabelfunktionen dargestellt werden, wie zum Beispiel die Strecke im freien Fall, der Weg einer gleichmäßig beschleunigten Bewegung, die kinetische Energie eines bewegten Körpers, der Energieinhalt eines Kondensators usw. Die nachfolgenden zwei Beispiele zeigen uns Situationen im Realleben. |
Beispiel 16Lösung 16Beispiel 17Lösung 17 per VideoLösung 17 verbal |
Quadratische Funktionen mit Parameter
| Bei Funktionen, deren Funktionsterm einen Parameter enthält – also eine zusätzliche Variable zu x - heißen Funktionen mit Parameter. Je nach Wert dieses Parameters – der Mathematiker bezeichnet diesen Parameter üblicherweise mit t - ändert sich der globale Verlauf des Graphen der Funktion in der Regel nicht, wohl aber ganz bestimmte Funktionswerte. Ein ganzrationaler Funktionsterm 2. Ordnung mit Parameter stellt eine Parabelschar dar. Die folgenden Beispiele stellen nur einen kleinen Einblick in die Funktionen mit Parameter dar. Weitere Aufgaben und Erläuterungen findest du in den Aufgabenblättern Level 3 / Expert. |
Beispiel 18LösungslogikLösungsaufschriebBeispiel 19LösungslogikLösungsaufschrieb |


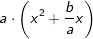 nicht einfach
nicht einfach 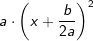 machen, denn, wenn wir diese binomische Formel nach den binomischen Regeln wieder auflösen, erhalten wir:
machen, denn, wenn wir diese binomische Formel nach den binomischen Regeln wieder auflösen, erhalten wir: 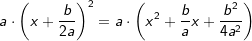 . Zwar entsprechen die ersten beiden Glieder
. Zwar entsprechen die ersten beiden Glieder 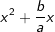 ja wieder den beiden Gliedern in der Klammer unserer Ausgangssituation
ja wieder den beiden Gliedern in der Klammer unserer Ausgangssituation 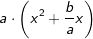 , allerdings ist jetzt wohl das
, allerdings ist jetzt wohl das 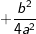 zu viel. Um dennoch weiterzukommen, ziehen wir also dieses
zu viel. Um dennoch weiterzukommen, ziehen wir also dieses 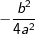 wieder ab, erhalten also:
wieder ab, erhalten also: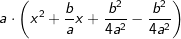 , was zweifelsohne dem Ausdruck
, was zweifelsohne dem Ausdruck 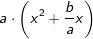 entspricht. Aus den ersten drei Gliedern
entspricht. Aus den ersten drei Gliedern 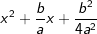 in der Klammer lässt sich nun aber eine binomische Formel bilden, sodass wir
in der Klammer lässt sich nun aber eine binomische Formel bilden, sodass wir 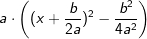 erhalten. Wenn wir jetzt diesen Ausdruck wieder ausmultiplizieren, erhalten wir
erhalten. Wenn wir jetzt diesen Ausdruck wieder ausmultiplizieren, erhalten wir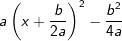 .
.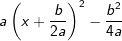 .Wir setzen diesen Ausdruck in f(x) ein und erhalten die endgültigen Scheitelform
.Wir setzen diesen Ausdruck in f(x) ein und erhalten die endgültigen Scheitelform 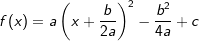 .
.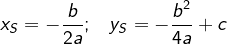 .
.



