Globales Verhalten

Globalverhalten gebrochen-rationaler Funktionen

Unter dem globalen Verhalten verstehen wir das Verhalten des Graphen einer Funktion an den Systemgrenzen. Wir verhält sich der Verlauf des Graphen für x nach -∞ und wie für x nach ∞. Bei den linearen und quadratischen Funktionen sowie bei den ganzrationalen Funktionen höheren Grades ist das Verhalten an den Systemgrenzen stets ein Unendliches.
Eine Gerade verläuft entweder aus dem III. Quadranten in den I. Quadranten oder aus dem II. Quadranten in den IV. Quadranten.
Eine Parabel verläuft entweder aus dem II. Quadranten in den I. Quadranten oder aus dem III. Quadranten in den IV. Quadranten.
Bei den ganzrationalen Funktionen höheren Grades ist dies ähnlich.
Bei den gebrochen-rationalen Funktionen ist das globale Verhalten ein asymptotisches Verhalten, welches wir im Folgenden näher untersuchen wollen.

Die waagrechte Asymptote

Beispiel 1

Gegeben ist die Funktion f mit 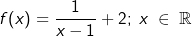$Fit in Mathe Latex: 93b266ab4be2cdf6d949f77f4a6ffaa5.png$ . Ihr Schaubild sei K. Bestimme den Verlauf von K im Unendlichen. Zeichne K in ein geeignetes Koordinatensystem und markiere das globale Verhalten.

Lösung 1

Wie bei den bisher kennengelernten Funktionen errechnen wir auch hier die Funktionswerte f(-∞) und f(∞). Wenn wir nun 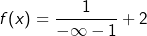$Fit in Mathe Latex: ed01b7c9187265d193eb522bb98ebc2c.png$ bilden, so wird ja die 1 im Zähler durch eine riesengroße negative Zahl dividiert, was im Endeffekt zu einem Grenzwert 0 des Bruches führt. Da diesem Grenzwert eine 2 hinzuaddiert wird, läuft der Funktionswert f(-∞) gegen 2. Die 2 ist also offensichtlich ein Grenzwert der Funktion f am linken Systemrand.
Ähnlich verhält es sich am rechten Systemrand. Mit 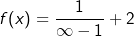$Fit in Mathe Latex: c1938b39b700e94d093132e07c120ddd.png$ wird die 1 im Zähler durch eine riesengroße positive Zahl dividiert, was wiederum zu einem Grenzwert 0 des Bruches und einem Grenzwert 2 der Funktion f am rechten Systemrand führt. In beiden Fällen nähert sich der Funktionswert der 2. Wir können somit schreiben:

$Fit in Mathe Latex: 83737ae7ba95872cdaa51bb5f48b48a0.png$

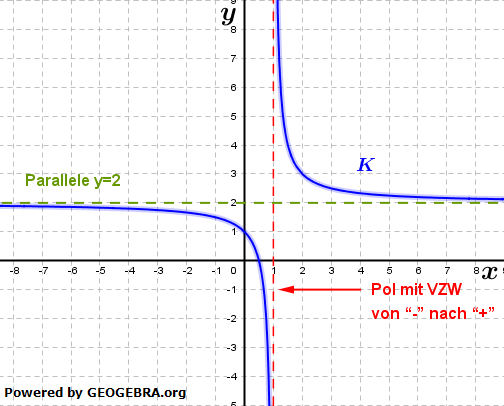
Die Kurve nähert sich im Unendlichen also einer Parallelen zur x–Achse im Abstand 2. Eine solche Parallele heißt waagrechte Asymptote.

Globalverhalten einer gebrochen rationalen Funmktion mit waagrechter Asymptote 1 (Analysis Funktionslehre WIKI Globalverhalten gebrochen-rationale Funktionen Graphik W0007/© by www.fit-in-mathe-online.de)

Beispiel 2

Gegeben ist die Funktion f mit 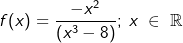$Fit in Mathe Latex: 809967528f4156eb0c60a4d5eeeffa61.png$ . Ihr Schaubild sei K. Bestimme den Verlauf von K im Unendlichen. Zeichne K in ein geeignetes Koordinatensystem und markiere das globale Verhalten.

Lösung 2

Zunächst erkennen wir bei dieser gebrochen-rationalen Funktion, dass sie eine Polstelle bei x₀=2 besitzt, bei diesem x–Wert wird der Nenner des Funktionsterms 0. Unsere Beispielfunktion hat nun sowohl im Zähler als auch im Nenner die Variable x stehen. Es ist eine echt gebrochen-rationale Funktion, da die Potenz des Zählers kleiner ist als die des Nenners.
Zur Bestimmung des asymptotischen Verhaltens am Systemrand müssen wir nun zuerst eine kleine Umformung des Funktionsterms vornehmen. Hierfür gibt es zwei Verfahren, die jedoch zum selben Ergebnis führen.

Verfahren 1: Ausklammern

	$Fit in Mathe Latex: 1b8e3c9c1cb383c88150be134b9e5e8f.png$
	Den so umgewandelten Term können wir nun um x² kürzen.
	$Fit in Mathe Latex: 701a7e95a6c6350dc5381b3a9b552fbf.png$
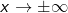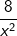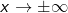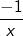	und überlegen uns erst jetzt, was an den Systemrändern passiert. Für $Fit in Mathe Latex: 477d65a0927001091617170db2ab2d36.png$ ist der Grenzwert des Restteils $Fit in Mathe Latex: ce541c28e99279c3f1e6f726877aee11.png$ im Nenner 0. Es verbleibt lediglich die Untersuchung, was für $Fit in Mathe Latex: 477d65a0927001091617170db2ab2d36.png$ mit dem Teilterm $Fit in Mathe Latex: b48c83c2590c1732c995b4c88395fcd6.png$ passiert. Und der läuft auch eindeutig auf die 0 zu. Wir können also schreiben:
	$Fit in Mathe Latex: 44c6b772a05e45d7a24ebf88a76a401b.png$
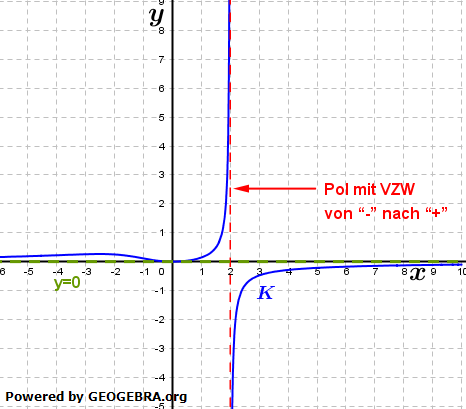
	Die Kurve nähert sich im Unendlichen also der x–Achse selbst, der Asymptoten y=0.

Verfahren 2: Kürzen

Globalverhalten einer gebrochen rationalen Funmktion mit waagrechter Asymptote 2 (Analysis Funktionslehre WIKI Globalverhalten gebrochen-rationale Funktionen Graphik W0008/© by www.fit-in-mathe-online.de)

Beispiel 3

Gegeben ist die Funktion f mit 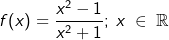$Fit in Mathe Latex: f868e901d5070876617d1cda731e6b1d.png$ . Ihr Schaubild sei K. Bestimme den Verlauf von K im Unendlichen. Zeichne K in ein geeignetes Koordinatensystem und markiere das globale Verhalten.

Lösung 3

Zunächst erkennen wir bei dieser gebrochen-rationalen Funktion, dass sie keine Polstelle besitzt, denn der Nenner x²+1 kann niemals 0 werden. Wie in Beispiel 2 klammern wir die höchste im Zähler vorkommenden Potenz von x aus.
	$Fit in Mathe Latex: 2af063d59c744ada74a9dcd3d80fa8c3.png$
und kürzen
	$Fit in Mathe Latex: c50927762cf04d3c6aacda006815bbe7.png$
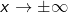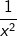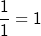Für $Fit in Mathe Latex: 4d4dc39c1c8f1f5fd1e32df855c8d43f.png$ ist der Grenzwert der Restteile $Fit in Mathe Latex: 8bdbd1a56f91cbee53511f0641648eab.png$ im Zähler und Nenner 0. Es verbleibt lediglich der Bruch $Fit in Mathe Latex: 33c33882576b0fdfea37ebc9a845580c.png$ . Der Graph der Funktion läuft im Unendlichen gegen 1. Wir können also schreiben:
	$Fit in Mathe Latex: be6f6de6464e0b9de1e75957d83d913d.png$
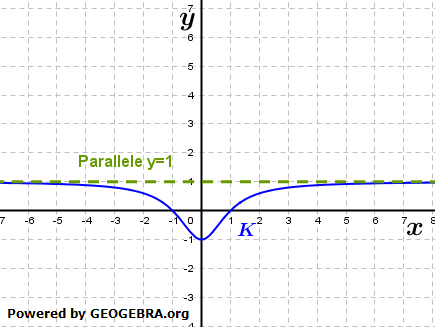
Die Kurve nähert sich im Unendlichen also einer Parallelen zur x–Achse im Abstand 1, der Asymptoten y=1.

Globalverhalten einer gebrochen rationalen Funmktion mit waagrechter Asymptote 3 (Analysis Funktionslehre WIKI Globalverhalten gebrochen-rationale Funktionen Graphik W0009/© by www.fit-in-mathe-online.de)

Die schiefe Asymptote

Beispiel 4

Gegeben ist die Funktion f mit 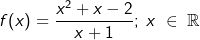$Fit in Mathe Latex: 7ed219ba604135479668e389cb9a6912.png$ . Ihr Schaubild sei K. Bestimme den Verlauf von K im Unendlichen. Zeichne K in ein geeignetes Koordinatensystem und markiere das globale Verhalten.

Lösung 4

Zunächst erkennen wir bei dieser gebrochen-rationalen Funktion, dass sie eine Polstelle bei x₀=-1 besitzt. Im Gegensatz zu Beispiel 1, Beispiel 2 und Beispiel 3 haben wir es mit einer unecht gebrochen-rationalen Funktion zu tun, denn die höchste Potenz von x im Zähler ist größer als die höchste Potenz von x im Nenner. Aus dem bislang Gelernten könnten wir jetzt folgern, dass der Zähler mit der höchsten Potenz x² schneller wächst als der Nenner mit der höchsten Potenz x¹ und die Kurve somit gegen ∞ läuft. 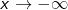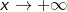Für $Fit in Mathe Latex: 002f73f7d0076dcc07e6834f51fe9fb2.png$ nach -∞ und für $Fit in Mathe Latex: d8c98851fb9561020db2866619be1309.png$ nach +∞. Die Kurve verläuft also aus dem III. Quadranten in den I. Quadranten. Für die Beschreibung des globalen Verhaltens würde dies zwar ausreichen, nicht aber für das asymptotische Verhalten. Unecht gebrochen-rationale Funktionen verfügen unter Umständen noch über eine schiefe Asymptote oder gar eine Näherungskurve im Unendlichen. Zur Feststellung dieses Verhaltens ist bei solchen Funktionstermen zunächst eine Polynomdivision erforderlich.

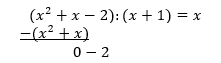Die Polynomdivision geht nicht auf, wir erhalten einen Rest von -2. Das Ergebnis der Division lässt sich somit auch schreiben:
	$Fit in Mathe Latex: f59e9cfb0c5197f15c2e062203e15079.png$
was zum geänderten Funktionsterm
	$Fit in Mathe Latex: 1ecee50419e462a4476ec0230eb4236f.png$
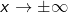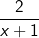führt. Erst jetzt dürfen wir die Grenzbetrachtung für $Fit in Mathe Latex: e5b2dfc83f22ceaa699441f683cb5280.png$ durchführen, wobei wir feststellen, dass dann ja der Restterm $Fit in Mathe Latex: 797314635b7a6dc21fb6b77133e0c714.png$ gegen 0 läuft. Die Kurve nähert sich im Unendlichen also immer mehr einer Geraden mit der Funktionsgleichung g(x)=x. Wir schreiben somit:
	$Fit in Mathe Latex: 11a690a0f17ed052e4e26692bdadd5ce.png$
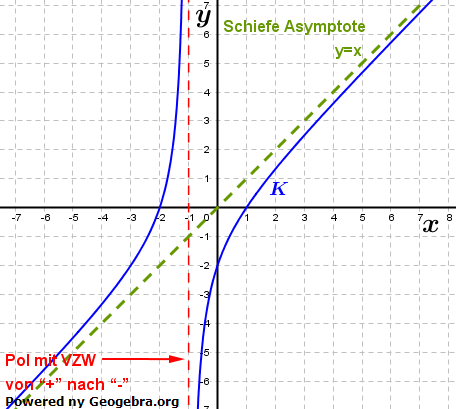
Die Kurve nähert sich im Unendlichen der schiefen Asymptote y=x.

Globalverhalten einer gebrochen rationalen Funmktion mit schiefer Asymptote (Analysis Funktionslehre WIKI Globalverhalten gebrochen-rationale Funktionen Graphik W0011/© by www.fit-in-mathe-online.de)

Näherungskurven

Beispiel 5

Gegeben ist die Funktion f mit 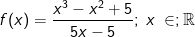$Fit in Mathe Latex: 29f8a037220936b2dcca1f2890aee964.png$ . Ihr Schaubild sei K. Bestimme den Verlauf von K im Unendlichen. Zeichne K in ein geeignetes Koordinatensystem und markiere das globale Verhalten.

Lösung 5

Zunächst erkennen wir bei dieser unecht gebrochen-rationalen Funktion, dass sie eine Polstelle bei x₀=1 besitzt. Wie in Beispiel 4 dargelegt, müssen wir für die Bestimmung des globalen Verhaltens eine Polynomdivision durchführen.

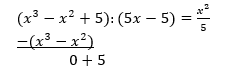Wir erhalten einen Rest 5 und können als Ergebnis schreiben
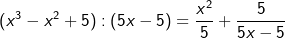	$Fit in Mathe Latex: a1b2a33fccef8f9bf5a15497935f1f18.png$ . Der geänderte Funktionsterm lautet:
	$Fit in Mathe Latex: 3cfc71ad5fb376e3de4f6df869761dca.png$
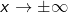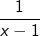Mit $Fit in Mathe Latex: e5b2dfc83f22ceaa699441f683cb5280.png$ läuft der Restterm $Fit in Mathe Latex: 590144eed24c0de8746a8654d5deea33.png$ gegen 0. Der Grenzwert der Funktion lautet:
	$Fit in Mathe Latex: 13f056e7d045256e1017a7da9d5d8e8a.png$
Die Kurve nähert sich im Unendlichen einer Näherungskurve, dem Graphen der Funktion f mit Funktionsgleichung $Fit in Mathe Latex: d90a753b7c573a5cd15264ae06552fb6.png$

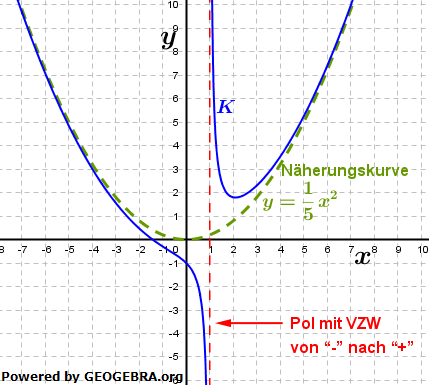Merksätze Globalverhalten gebrochen-rationale Funktionen

Merksatz allgemein Globalverhalten gebrochen-rational

Das globale Verhalten von gebrochen-rationalen Funktionen ist asymptotisch.
Echt gebrochen-rationale Funktionen haben stets eine waagrechte Asymptote, also entweder die x–Achse selbst oder eine Parallele zur x–Achse. Zur Feststellung der Gleichung dieser Asymptote muss der Funktionsterm zunächst entweder durch Ausklammern der kleinsten Potenz von x im Zähler oder durch Kürzen des Funktionsterms mit der kleinsten Potenz von x im Zähler verändert werden.
Unecht gebrochen-rationale Funktionen verlaufen an den Systemgrenzen ins Unendliche. Sie verfügen in der Regel jedoch entweder über eine Gerade (schiefe Asymptote) oder über eine Kurve (Näherungskurve). Zur Feststellung der Gleichung der schiefen Asymptote bzw. Näherungskurve muss der Funktionsterm zunächst durch Polynomdivision mit Restanteil verändert werden.

Schnellmerksatz Globalverhalten gebrochen-rational

	Sei $Fit in Mathe Latex: 0bb7f0459f5b9b2aa3c501d654949581.png$
		die gebrochen-rationale Funktion, dann gilt:
	Fall 1:	n < m Die höchste Potenz des Zählers (n) ist kleiner als die höchste Potenz des Nenners (m): Gleichung der Asymptoten lautet y = c.
	Fall 2:	n = m Die höchste Potenz des Zählers (n) ist gleich der höchsten Potenz des Nenners (m): Gleichung der Asymptoten lautet $Fit in Mathe Latex: 24244a561030b555f61eda1d15230452.png$
	Fall 3:	n = m+1 Die höchste Potenz des Zählers (n) ist um 1 größer als die höchste Potenz des Nenners (m): Die Gleichung der Asymptoten muss per Polynomdivision ermittelt werden, der Graph der Funktion hat eine schiefe Asymptote.
	Fall 4:	n > m+1 Die höchste Potenz des Zählers (n) ist um mehr als 1 größer als die höchste Potenz des Nenners (m): Die Gleichung der Asymptoten muss per Polynomdivision ermittelt werden, der Graph der Funktion hat eine Näherungskurve.

	Der Funktionsterm wird mit der höchsten im Zähler vorkommenden Potenz von x gekürzt. In unserem Beispiel ist dies x².
	$Fit in Mathe Latex: 37bda12e65b46f582c717ebe5b600312.png$
	Die restliche Betrachtung ist nun identisch mit Verfahren 1.