 |
Potenzfunktionen der Funktionsklassen |


Die Potenzfunktion f(x)=a⋅(x-b)q+c
| Unter Potenzfunktionen verstehen wir Funktionen mit einem einzelnen x-Glied welches eine rationale Potenz aufweist. Die allgemeinen Form einer Potenzfunktion lautet: |
| f(x)=a(x-b)q+c. |
| q ist dabei jede beliebige rationale Zahl, also ganzzahlig positiv, ganzzahlig negativ, oder eine Dezimalzahl bzw. ein endlicher Bruch. |
Auswirkung des Parameters q
Ganzzahlige, positive und gerade Werte von q
Ganzzahlige, positive und ungerade Werte von q
Ganzzahlige, negative und gerade Werte von q
Ganzzahlige, negative und ungerade Werte von q
Rationale, positive Werte von q
Rationale, negative Werte von q
Auswirkung des Parameters b
Auswirkung des Parameters c
Definitions- und Wertebereich von Potenzfunktionen
| Definitions- und Wertebereich (auch Definitionsmenge bzw. Wertemenge genannt) von Funktionen bestimmen den Verlauf des Graphen einer Funktion, so auch bei den Potenzfunktionen. Zur Erinnerung hier noch einmal die Definition der beiden Bereiche: |
Definitionsbereich (Definitionsmenge)
Wertebereich (Wertemenge)
Beispiele
Beispiel 1
Lösung 1
Beispiel 2
Lösung 2
Beispiel 3
Lösung 3
Beispiel 4
Lösung 4
Beispiel 5
Lösung 5
Beispiel 6
Lösung 6
Symmetrien von Potenzfunktionen
| Auch Potenzfunktionen haben ein Symmetrieverhalten. Die nachfolgende Übersicht zeigt dir, bei welcher Art von Potenzfunktion welche Symmetrie vorliegt. Detaillierte Information über Symmetrien findest du im Kapitel |
| „Graphen und Funktionen analysieren“ |
| hier im Portal. Symmetrien der Funktion f mit 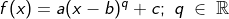 . . |
Symmetrieverhalten für  und
und 
| Potenzfunktionen Aufgabenblatt Level 1 / Blatt 1 27 Aufgaben im Blatt |
| Potenzfunktionen Aufgabenblatt Level 1 / Blatt 2 32 Aufgaben im Blatt |
| Potenzfunktionen Aufgabenblatt Level 2 / Blatt 1 41 Aufgaben im Blatt |
| Potenzfunktionen Aufgabenblatt Level 2 / Blatt 2 23 Aufgaben im Blatt |
| Potenzfunktionen Aufgabenblatt Level 3 / Blatt 1 25 Aufgaben im Blatt |





