 |
WIKI Funktionsanalyse - Kurvendiskussion |


Funktionen analysieren
| Unter „Funktionsanalyse“ bzw. "Kurvendiskussion" in der Differenzialrechnung wollen wir die Untersuchung der Graphen von Funktionen auf deren geometrische Eigenschaften, wie zum Beispiel Schnittpunkte mit den Koordinatenachsen, Hoch- und Tiefpunkte, Wendepunkte, gegebenenfalls Sattel- und Flachpunkte, Asymptoten, Verhalten im Unendlichen (Globalverhalten) u.a.m. verstehen. Diese Informationen erlauben es uns, eine Skizze des Graphen anzufertigen, aus der all diese für die Funktion charakteristischen Eigenschaften unmittelbar ablesbar sind. Heute ist es nicht mehr das Ziel einer Kurvendiskussion, den Menschen dabei zu unterstützen, eine möglichst genaue Zeichnung des Graphen der Funktion zu produzieren: das kann inzwischen jeder Funktionsplotter (etwa ein grafikfähiger Taschenrechner, ein Smartphone mit entsprechender Software, ein Tabellenkalkulationsprogramm oder Computeralgebra-Software) besser. |
|
Ziel der Kurvendiskussion ist vielmehr,
Quelle: angelehnt an WIKIPEDIA Kurvendiskussion |
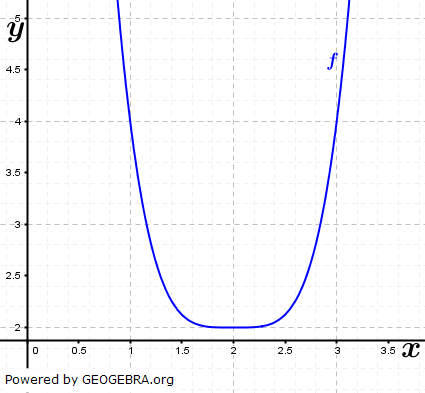 Abbildung 1 Abbildung 10 ≤ x ≤ 3,5; 0 ≤ y ≤ 5 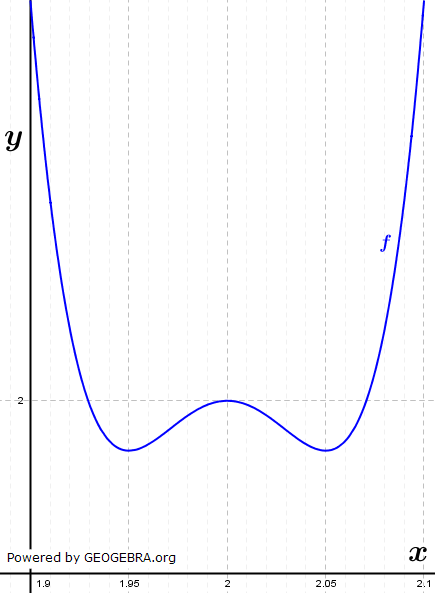 Abbildung 2 Abbildung 21,9 ≤ x ≤ 2,1; 1,95 ≤ y ≤ 2,15 |
Elemente der Kurvendiskussion
Globalverhalten
| Um das Verhalten im Unendlichen herauszufinden, untersuchen wir den Funktionswert einer Funktion f(x) wenn x über alle Grenzen wächst, also gegen den Wert x→∞ läuft. Entsprechendes gilt auch für x→-∞. Nähere Einzelheiten und Beispiele findest du im Kapitel „Globalverhalten“. |
Schnittpunkte mit den Koordinatenachsen
| Schnittpunkte mit den Koordinatenachsen sind zum einen der Schnittpunkt des Graphen einer Funktion mit der y-Achse und zum anderen die Schnittpunkte des Graphen einer Funktion mit der x-Ache. Es gibt maximal einen Schnittpunkt mit der y-Achse. Schnittpunkte mit der x-Achse – auch Nullstellen genannt – können mehrfach vorkommen. Die ist abhängig von der Klasse der Funktion. |
| Um die Nullstellen einer Funktion f(x) und damit die Schnittpunkte des Funktionsgraphen mit der x-Achse zu finden, wird die Lösungsmenge der Gleichung f(x)=0 berechnet. Die genaue Vorgehensweise hängt davon ab, welche Funktion untersucht wird. Ist die Funktion f beispielsweise durch einen Bruchterm gegeben, so wird der Zähler gleich 0 gesetzt, um die Nullstellen zu erhalten. Um den Schnittpunkt des Funktionsgraphen mit der y-Achse zu bestimmen, wird für x der Wert 0 eingesetzt. Der y-Achsenabschnitt liegt dann folglich bei Sy(0|f(0)). Nähere Einzelheiten und Beispiele findest du im Kapitel „Schnittpunkte mit den Koordinatenachsen“. |
Symmetrieverhalten
| Bei der Beantwortung der Frage, ob der Graph der gegebenen Funktion in irgendeiner Weise symmetrisch ist, müssen mehrere Fälle berücksichtigt werden. | ||
| • | Achsensymmetrie bezüglich der y-Achse | |
| Der Graph einer Funktionist genau dann achsensymmetrisch bezüglich der y-Achse, wenn für beliebige x-Werte des Definitionsbereiches gilt: f(-x)=f(x) |
||
| Bei ganzrationalen Funktionen bedeutet diese Bedingung, dass nur gerade Exponenten auftreten. | ||
| • | Punktsymmetrie bezüglich des Ursprungs | |
| Der Graph einer Funktion f ist genau dann punktsymmetrisch bezüglich des Ursprungs, wenn für beliebige x-Werte des Definitionsbereiches gilt: f(-x)=-f(x) ==> -f(-x)=f(x) |
||
| Der Graph einer ganzrationalen Funktion ist genau dann punktsymmetrisch bezüglich des Ursprungs, wenn nur ungerade Exponenten vorkommen. | ||
| • | Achsensymmetrie bezüglich einer beliebigen Achse | |
| Achsensymmetrie bezüglich einer Geraden mit der Gleichung x=x0 parallel zur y-Achse lässt sich überprüfen mithilfe der Bedingung: f(x0-h)=f(x0+h) |
||
| Achsensymmetrisch sind unter anderem die Graphen der quadratischen Funktionen. Die Symmetrieachse ergibt sich in diesem Fall aus der x-Koordinate des Scheitels. | ||
| • | Punktsymmetrie bezüglich eines beliebigen Zentrums | |
| Die Bedingung für Punktsymmetrie bezüglich des Punktes P(x0│y0) lautet: f(x0-h)+f(x0+h)=2⋅y0 oder äquivalent f(x0+h)-y0=y0-f(x0-h) |
||
| Die Graphen aller kubischen Funktionen sind punktsymmetrisch. Das Symmetriezentrum ist jeweils der (einzige) Wendepunkt. | ||
| Nähere Einzelheiten und Beispiele findest du im Kapitel „Symmetrieverhalten“. | ||
Extrempunkte (Hoch- und Tiefpunkte)
| Um die Extrempunkte – das heißt Hoch- und Tiefpunkte – einer stetig differenzierbaren Funktion f zu bestimmen, wird die erste Ableitung von f gleich 0 gesetzt, das heißt, die Lösungsmenge der Gleichung f'(x)=0 wird berechnet. Alle Lösungen dieser Gleichung sind mögliche sogenannte Extremstellen. Die Bedingung f'(x)=0 ist allerdings nur eine notwendige Bedingung für Extremstellen. Eine Stelle mit der Steigung 0 könnte auch ein Sattelpunkt sein. Das Standardbeispiel ist f(x)=x3 an der Stelle 0. Obwohl f'(x)=0 gilt, ist der Punkt O(0|0) kein Extrempunkt, sondern ein Sattelpunkt. Zum Nachweis der Extrempunkteigenschaften benötigen wir daher eine der im Folgenden genannten hinreichenden Bedingungen: |
|||
| • | Hinreichende Bedingung 1: Wert der zweiten Ableitung | ||
| Diese Bedingung bietet eine bequeme Möglichkeit, den Nachweis für ein relatives Extremum zu führen und zugleich die Art (Maximum oder Minimum) zu bestimmen. Es gilt: Sei x0 eine ermittelte Nullstelle der ersten Ableitung f', so ist der Punkt P(x0│f(x0)) Hochpunkt, sofern f''(x0)<0; Tiefpunkt, sofern f''(x0 )>0; Weder noch, sofern f''(x0 )=0. |
|||
| • | Hinreichende Bedingung 2: Vorzeichen der ersten Ableitung | ||
| Ein zweites (umständlicheres) Verfahren zum Nachweis der Extrempunkteigenschaft kommt ohne die Berechnung der zweiten Ableitung aus. Es wird untersucht, ob die erste Ableitung f' an der betrachteten Stelle x0 ihr Vorzeichen wechselt. Diese Methode lässt sich folgendermaßen anschaulich deuten: Durchläuft man den Funktionsgraphen in der Umgebung eines Hochpunktes von links nach rechts, so lässt sich das Aussehen dieser Kurve wie folgt beschreiben: |
|||
| 1. | Links vom Hochpunkt steigt der Funktionsgraph an. Die Steigung ist positiv. | ||
| 2. | Im Hochpunkt selbst verläuft die Tangente waagerecht. Die Steigung ist 0. | ||
| 3. | Rechts vom Hochpunkt fällt der Funktionsgraph. Die Steigung ist negativ. | ||
| Entsprechendes gilt, nur umgekehrt, für Tiefpunkte. | |||
| Nähere Einzelheiten und Beispiele findest du im Kapitel „Extrempunkte (Hoch- und Tiefpunkte)“. | |||
Wendepunkte
| Als Wendepunkte bezeichnen wir diejenigen Punkte, in denen der gegebene Funktionsgraph seine Steigung von stärker nach flacher bzw. von flacher nach stärker wechselt. Dies gilt sowohl für positive als auch für negative Steigungen und wird auch mit Links- Rechtskrümmungswechsel bzw. Rechts- Linkskrümmungswechsel bezeichnet. Zur Bestimmung der Wendepunkte setzen wir zunächst die zweite Ableitung gleich 0. Die Lösungen der Gleichung f''(x)=0 (siehe notwendige Bedingung) kommen als Wendestellen in Frage. Mit einer der nachfolgend aufgeführten hinreichenden Bedingungen weisen wir anschließend nach, dass tatsächlich ein Wendepunkt vorliegt. |
||
| • | Notwendige Bedingung | |
| Sei f eine reelle Funktion, die in einem offenen Intervall I definiert und zweimal stetig differenzierbar ist. Hat der Graph von f an der Stelle x0 einen Wendepunkt, so gilt f''(x0)=0. | ||
| • | Hinreichende Bedingung 1: Wert der dritten Aleitung | |
| Diese Bedingung bietet eine bequeme Möglichkeit, den Nachweis für das Vorliegen eines Wendepunktes zu führen und zugleich den Wechsel der Krümmung von rechts nach links bzw. von links nach rechts festzustellen. Sei f eine reelle Funktion, die in einem offenen Intervall I definiert und dreimal stetig differenzierbar ist, und gilt an der der Stelle 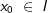 1. f'' (x0)=0 2. f''' (x0)≠0 so hat der Graph von f an der Stelle x0 eine Wendestelle. |
||
| • | Hinreichende Bedingung 2: Wert der ersten Aleitung | |
| Ist an der Stelle x0 neben der zweiten Ableitung auch die dritte Ableitung gleich 0, so versagt das zuletzt genannte Kriterium. In diesem Fall untersuchen wir, ob die erste Ableitung bei x0 das Vorzeichen wechselt. Zu diesem Zweck wählen wir einen Wert kleiner und einen Wert größer als die Nullstelle der zweiten Ableitung (also der x-Koordinate der eventuellen Wendestelle). Diese beiden Werte werden in die erste Ableitung eingesetzt. Unterscheiden sich die Vorzeichen der Werte der ersten Ableitung an diesen Stellen, so liegt kein Wendepunkt vor. Wechselt das Vorzeichen nicht, so handelt es sich um eine Wendestelle. |
||
| Nähere Einzelheiten und Beispiele findest du im Kapitel „Wendepunkte“. | ||
Monotonie und Krümmung
| Nachdem ins die notwendigen Bedingungen für Extrem- und Wendepunkte bekannt sind, können wir Aussage über das Monotonie- als auch das Krümmungsverhalten eines Graphen von f machen. Hierbei gilt: | |
| • | Monotonieverhalten |
| Das Monotonieverhalten eines Graphen von f wechselt von steigend auf fallend bzw. umgekehrt in den Extrempunkten. Links eines Hochpunktes bzw. rechts eines Tiefpunktes ist der Graph monoton steigend. Rechts eines Hochpunktes bzw. links eines Tiefpunktes ist der Graph monoton fallend. Monotonie ist somit ein Verhalten innerhalb eines Intervalls I. Kommen innerhalb dieses Intervalls Steigungswerte von f nur ein einziges Mal vor, so sagen wir „streng monoton steigend“ (bzw. fallend), sonst sagen „monoton steigend“ (bzw. fallend). |
|
| • | Krümmungsverhalten |
| Das Krümmungsverhalten eines Graphen von f wechselt in den Wendepunkten. Wir sprechen von Linkskrümmung und Rechtskrümmung alternativ linksdrehend bzw. rechtsdrehend. Der Graph einer Funktion f ist rechts gekrümmt, wenn sich der Verlauf des Graphen im Uhrzeigersinn dreht. Dies ist der Fall, wenn sich die Steigung von größer auf kleiner ändert. Der Graph einer Funktion f ist links gekrümmt, wenn sich der Verlauf des Graphen gegen den Uhrzeigersinn dreht. Dies ist der Fall, wenn sich die Steigung von kleiner auf größer ändert. |
|
| Nähere Einzelheiten und Beispiele findest du im Kapitel „Monotonie und Krümmung“. | |
Asymptoten
| Wir unterscheiden nach waagrechten, schiefen und senkrechten Asymptoten. Eine weitere Unterscheidungsklasse sind Näherungskurven. Die senkrechten Asymptoten haben einen weiteren Namen, sie werden auch als Pole bezeichnet. | ||
| • | Waagrechte Asymptoten |
|
Eine waagrechte Asymptote liegt vor, wenn sich der Funktionswert einer Funktion f im Unendlichen einem bestimmten Wert 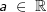 nähert. Wir schreiben: nähert. Wir schreiben: 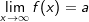 , alternativ , alternativ 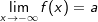 . . |
||
| • | Schiefe Asymptoten |
|
Eine schiefe Asymptote liegt vor, wenn sich der Funktionswert einer Funktion f im Unendlichen einer Geraden y=m⋅x+c nähert. Wir schreiben: 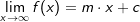 , alternativ , alternativ 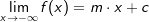 . . |
||
| • | Näherungskurven | |
Eine Näherungskurve liegt vor, wenn sich der Funktionswert einer Funktion f im Unendlichen einer anderen Funktion g nähert. Wir schreiben: 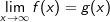 , alternativ , alternativ 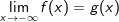 . . |
||
| • | Senkrechte Asymptoten (Pole) | |
| Senkrechte Asymptoten treten nur in Definitionslücken auf, z. B. bei gebrochen rationalen Funktionen. In Definitionslücken von Funktionen nimmt die Abszisse x einen Wert an, der zu einer Division mit 0 führt. Eine senkrechte Asymptote wird kürzer auch mit Pol bezeichnet. Bei Annäherung des Wertes der Abszisse x an die Definitionslücke läuft der Funktionswert entweder gegen +∞ oder -∞. Gegen Welchen Wert er läuft ist abhängig von der Funktionsgleichung und ist von Fall zu Fall zu untersuchen. Wir unterscheiden noch Pole mit Vorzeichenwechsel und ohne Vorzeichenwechsel. |
||
| Nähere Einzelheiten und Beispiele findest du im Kapitel „Asymptoten“. | ||
| Du befindest dich hier: |
| WIKI Funktionsanalyse - Kurvendiskussion |



