 |
WIKI zum Logarithmus
|

Einführung
| Als Logarithmus (Plural: Logarithmen; von altgriechisch λόγος lógos, „Verständnis, Lehre, Verhältnis“, und ἀριθμός, arithmós, „Zahl“) einer Zahl bezeichnet man den Exponenten, mit dem eine vorher festgelegte Zahl, die Basis, potenziert werden muss, um die gegebene Zahl, den Numerus, zu erhalten. | 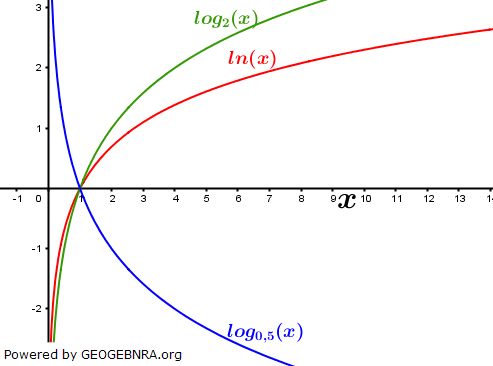 Graphen unterschiedlicher Logarithmusfunktionen |
| Logarithmen sind nur für positive reelle Zahlen definiert, auch die Basis muss positiv sein. Der Logarithmus einer positiven reellen Zahl x zur Basis b ist also der Wert des Exponenten, wenn x als Potenz zur Basis b dargestellt wird, also diejenige Zahl y, welche die Gleichung by=x löst. Man schreibt y=logb(x). Das Logarithmieren, d. h. der Übergang von x zu logb(x), ist damit eine Umkehroperation des Potenzierens. Die Funktion, die bei gegebener fester Basis b jeder positiven Zahl ihren Logarithmus zuordnet, nennt man Logarithmusfunktion zur Basis b. |
|
| Mit Logarithmen lassen sich sehr stark wachsende Zahlenreihen übersichtlich darstellen, da der Logarithmus für große Zahlen viel langsamer steigt als die Zahlen selbst. Wie die Gleichung |  Spiralförmiges Schneckenhaus 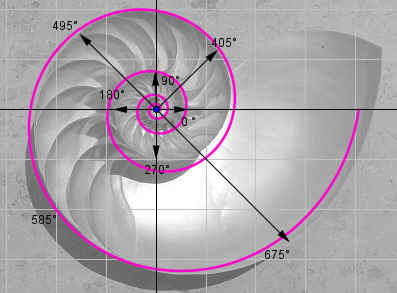 Graph einer logarithmischen Spirale. |
| logb(x⋅y)=logb(x)+logb(y) | |
| zeigt, kann man durch Logarithmieren eine Multiplikation durch die viel weniger rechenintensive Addition ersetzen. Auch beschreiben Logarithmen auf mathematisch elegante Weise viele technische Prozesse sowie Phänomene der Natur wie etwa das Verhalten einer Halbleiter-Diode, die Spirale eines Schneckenhauses (siehe Grafiken rechts) oder die | |
| Wahrnehmung unterschiedlicher Lautstärken durch das menschliche Ohr. | |
Potenz, Wurzel, Logarithmus
| Es gibt einen unmittelbaren Zusammenhang zwischen Potenzen und Wurzeln sowie zwischen Potenzen und Logarithmen. Beide Rechenarten – Wurzeln und Logarithmen – sind Umkehrrechenarten des potenzierens. Doch wo ist der Unterschied? |
Potenz und Wurzel
Diesen Zusammenhang haben wir im Kapitel „Wurzeln“ bereits ausführlich behandelt. Wir wissen, dass für 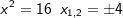 , somit die beiden Werte x1=4 sowie x2=-4 Lösungen der Gleichung sind. Oder bei , somit die beiden Werte x1=4 sowie x2=-4 Lösungen der Gleichung sind. Oder bei 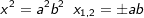 sind x1=ab und x2=-ab Lösungen. Wir müssen bei der Potenz x2 die Wurzel ziehen, um zu wissen wie große denn x ist. sind x1=ab und x2=-ab Lösungen. Wir müssen bei der Potenz x2 die Wurzel ziehen, um zu wissen wie große denn x ist. |
Potenz und Logarithmus
| Bislang haben wir nur Potenzen kennengelernt, bei denen die Variable x die Basis der Potenz dartstellte und der Exponent eine Zahl aus der Menge der rationalen Zahlen war. Nun kann es aber doch auich umgekehrt sein, die Basis einer Potenz ist eine Zahl aus der Menge der rationalen Zahlen und der Exponent ist die Variable x. |
|
| Beispiel: | |
| 2x=16 Wir wollen jetzt wissen, wie groß muss denn der Exponent x sein, damit 2x=16 ergibt, also wie oft müssen wir die Zahl 2 mit sich selbst multipizieren, damit 16 herauskommt. Nun, bei diesem Beispiel ist es noch einfach, denn wir erkennen sofort, das 2⋅2⋅2⋅2=16 ist, also muss x=4 sein. |
|
| Somit haben wir es hier zwar auch mit einer Umkehrrechenart des Potenzierens zu tun, die Vorgehensweise ist aber eine ganz andere, denn bei 2x=16 könnten wir zwar gemäß den Regeln zur Äquvalenzumformung schreiben: | |
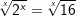 ⇒ ⇒ 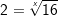 |
|
| Aber welche Wurzel sollen wir denn jetzt ziehen? Was ist denn die x-te Wurzel? |
|
| Ist die Basis einer Potenz eine Zahl der rationalen Zahlenmenge und der Exponent die Variable / Unbekannte, so müssen wir die Logarithmusrechnung zur Lösung einer solchen Gleichung anwenden. | |
Die einzelnen Kapitel des Logarithmus
Machen wir uns einen Überblick über die behandelten einzelnen Kapitel im Portal.
Der Logarithmus einer Zahl
| Unter dem Logarithmus verstehen wir eine Zahl, mit der man die Basis des Logarithmus potenzieren muss, um die Zahl zu erhalten. Wir schreiben | |
| loga(b)=x | |
| In dieser Schreibweise ist a die Basis der Potenz, b die zu erhaltende Zahl und x die gesuchte Potenz zur Basis a. | |
| Beispiele: | |
| log2(16)=x: | x ist die Zahl, mit der man die 2 potenzieren muss, um 16 zu erhalten. |
| log3(243)=x: | x ist die Zahl, mit der man die 3 potenzieren muss, um 243 zu erhalten. |
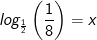 : : |
x ist die Zahl, mit der man  potenzieren muss, um potenzieren muss, um  zu erhalten. zu erhalten. |
Die Logarithmengesetze
Wir betrachten hier lediglich die Form der einzelnen Logarithmengesetze.
Vertiefende Betrachtungen und Übungsaufgaben findest du im diesbezüglichen Kapitel.
Vertiefende Betrachtungen und Übungsaufgaben findest du im diesbezüglichen Kapitel.
Logarithmus eines Produktes
Für den Logarithmus eines Produkts gilt:
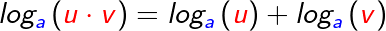
Umgekehrt gilt somit
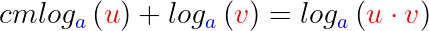
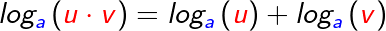
Umgekehrt gilt somit
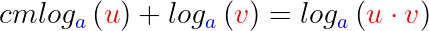
Logarithmus eines Quotienten
Für den Logarithmus eines Quotienten gilt:
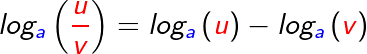
Umgekehrt gilt somit

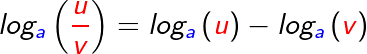
Umgekehrt gilt somit

Logarithmus einer Potenz
Für den Logarithmus einer Potenz gilt:
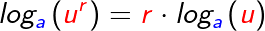
Umgekehrt gilt somit
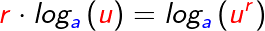
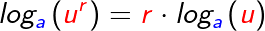
Umgekehrt gilt somit
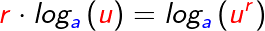
Logarithmus Sonderregeln
Es existieren drei besondere Regeln, die du auswendig lernen solltest:
1. Sonderregel

Jeder Logarithmus von seiner Basis ist immer 1.
2. Sonderregel

Jeder Logarithmus von 1 ist stets 0.
3. Sonderregel
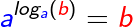
Logarithmen als Potenz ihrer Basis heben sich auf.
1. Sonderregel

Jeder Logarithmus von seiner Basis ist immer 1.
2. Sonderregel

Jeder Logarithmus von 1 ist stets 0.
3. Sonderregel
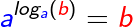
Logarithmen als Potenz ihrer Basis heben sich auf.
Berechnungen mit Logarithmen
| Der Logarithmus einer Zahl kann nicht nur durch „Probieren“ gefunden werden, sondern konkret auch durch Berechnungen. Da die meisten Logarithmuszahlen jedoch irrationale Zahlen sind, ist die Verwendung eines Taschenrechners unumgänglich. In Zeiten, in denen es noch keine elektronischen Taschenrechner gab, halfen umfangreiche Tabellen. Da jedoch jede rationale, positive Zahl außer der 1 die Basis eines Logarithmus sein kann, gibt es unendlich viele Logarithmensysteme. In der Praxis haben sich zwei Systeme durchgesetzt, nämlich das des dekadischen Logarithmus, also des Logarithmus zur Basis 10 und der natürliche Logarithmus, der Logarithmus zur Basis e, der Eulerschen Zahl. Diese beiden Logarithmensysteme haben auch eine eigene Schreibweise. Ist der dekadische Logarithmus – ausgeschrieben als log10(b) – gemeint, wird vereinfacht nur log(b) bzw. lg(b) geschrieben. Auf den heutigen elektronischen Taschenrechnern jeglicher Art finden wir eine mit log beschriftete Taste. Diese Taste berechnet den Logarithmus zur Basis 10. Ist der natürliche Logarithmus - loge(b) – gemeint, wird nur ln(b) geschrieben (Die Abkürzung steht für logarithmus naturalis). Auf den heutigen elektronischen Taschenrechnern jeglicher Art finden wir eine mit ln beschriftete Taste. Diese Taste berechnet den Logarithmus zur Basis e. |
Logarithmische Gleichungen
| Mit der Beziehung loga(b)=c lassen sich drei unterschiedliche Arten von Bestimmungsgleichungen aufstellen. Die Frage nach dem Logarithmuswert führt mit x als gesuchtem Wert auf eine Gleichung der Form |
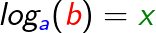 |
| Die Frage nach der Basis führt mit x als gesuchtem Wert auf eine Gleichung der Form |
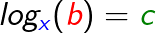 |
| Die Frage nach der Numerus führt mit x als gesuchtem Wert auf eine Gleichung der Form |
 |
| Rechenregelen, Beispiel und Aufgaben hierzu findest du im Kapitel Logaritmische Gleichungen. |
| Du befindest dich hier: |
| WIKI zum Logarithmus |



