 |
Ganzrationale Funktionen der Funktionsklassen |
Die Ganzrationale Funktion f(x)=an⋅xn+an-1⋅xn-1+an-2⋅xn-2+...+a1⋅x+a0
| Ganzrationale Funktionen der Funktionsklassen sind zusammengesetzte Funktionen, deren einzelne Glieder wiederum aus Potenzfunktionen mit ganzzahlig positivem Exponenten bestehen. Die allgemeinen Form einer Ganzrationalen Funktion lautet: |
| f(x)=an⋅xn+an-1⋅xn-1+an-2⋅xn-2+...+a1⋅x+a0. |
| n ist höchste Potenz, n-1 ist die um 1 verminderte höchste Potenz, n-2 die um 2 verminderte höchste Potenz usw bis zur Potenz 1 bei a1x. Am Ende der Funktionsgleichung steht dann das absolute Glied a0. Die a-Werte in der Gleichung werden als Koeffizienten bezeichnet. Alle a sind Element von 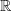 . Die Indices von an, an-1, an-2 usw. verweisen auf die Teilfunktion mit dem entsprechenden n als Exponent. |
Klassifizierung ganzrationaler Funktionen, Definitionsmenge
| Entsprechend der höchsten Potenz n von x wird den ganzrationalen Funktionen ein Grad zugesprochen. Ist n=3, so handelt es sich um eine ganzrationale Funktion 3. Grades. Ist n=4, so handelt es sich um eine ganzrationale Funktion 4. Grades. Ganzrationale Funktionen werden auch Polynome oder (seltener für Funktionen mit einem Grad größer 2) Parabeln genannt. Der Nullfunktion f mit f(x)=0 (für alle reellen Werte von x) wird kein Grad zugeordnet. Die maximale Definitionsmenge einer ganzrationalen Funktion ist  . |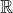
|
Merksatz Definition ganzrationaler Funktionen
|
Auswirkung des Exponenten n
Auswirkung des Koeffizienten an
Auswirkung des absoluten Gliedes a0
| Du befindest dich hier: |
| Ganzrationale Funktionen der Funktionsklassen |
