 |
Gebrochen-rationale Funktionen der Funktionsklassen |
Einführung
| Gebrochen rationale Funktionen sind Funktionen, deren Funktionsterm aus dem Quotienten zweier Polynome gebildet ist. In Kurzschreibweise schreiben wir: |
 . |
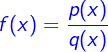| Die vollständige Schreibweise lautet: |
 |
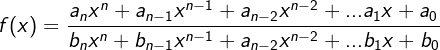| Der Funktionsterm einer Geraden, einer Parabel oder eines Polynoms höheren Grades wird durch den Funktionsterm einer Geraden, einer Parabel oder einer Polynoms dividiert und bildet dadurch die gebrochen-rationale Funktion. |
| Wir unterscheiden zwei Arten von gebrochen-rationalen Funktionen, die echt gebrochenen und die unecht gebrochenen rationalen Funktionen. Analog der Bruchrechnung mit echten und unechten Brüchen ist bei den echt gebrochen- rationalen Funktionen die höchste im Zähler vorkommende Potenz von x kleiner als die höchste im Nenner vorkommende Potenz von x. Bei den unecht gebrochen- rationalen Funktionen ist dies umgekehrt. |
Beispiel 1
Gegeben ist die Funktion f mit 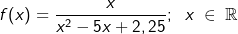 . Ihr Schaubild sei K. Zeichne die Funktion in ein geeignetes Koordinatensystem. |
Lösung 1
 |
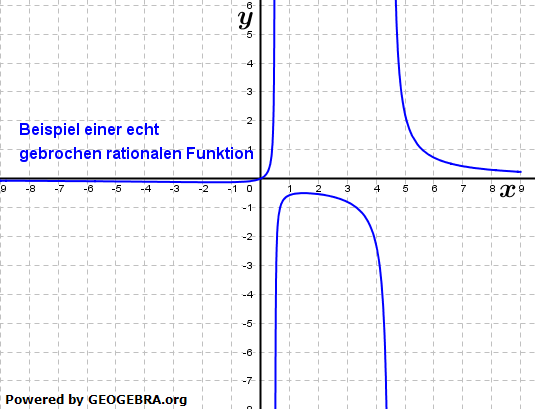| Wir erkennen im Funktionsterm, dass die im Zähler höchste vorkommende Potenz von x (nämlich hier 1) kleiner als die höchste im Nenner vorkommende Potenz von x (hier 2) ist. |
Beispiel 2
Gegeben ist die Funktion f mit 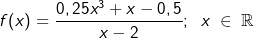 . Ihr Schaubild sei K. Zeichne die Funktion in ein geeignetes Koordinatensystem. |
Lösung 2
 |
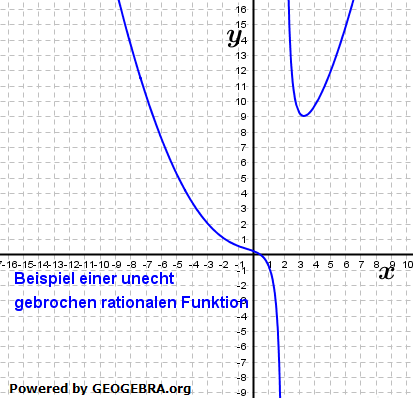| Wir erkennen im Funktionsterm, dass die im Zähler höchste vorkommende Potenz von x (nämlich hier 1) kleiner als die höchste im Nenner vorkommende Potenz von x (hier 2) ist. |
| Merksatz gebrochen rationale Funktion
|
||||
.Ganzrationale Funktionen Aufgabenblatt Level 1 / Blatt 1  xx Aufgaben im Blatt |
| Du befindest dich hier: |
| Gebrochen-rationale Funktionen der Funktionsklassen |
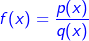