 |
|
WIKI zu Zinseszinsen
|


Die Zinseszinsrechnung
| Die Zinseszinsrechnung beschäftigt sich mit der Berechnung des Zinseszinses in Abhängigkeit vom Zinssatz sowie der Höhe und Dauer einer Kapitalanlage. Sie ist Teilgebiet der Finanzmathematik. |
| Haben wir im Kapitel „Zinsen“ gelernt, was Zinsen überhaupt sind und wie sie sich berechnen, wenn wir einen Zeitraum von maximal einem Jahr nicht überschreiten, wollen wir uns nun einen Zeitraum von mehr als einem Jahr betrachten. |
| Wird ein Kapital bei einer Bank mehr als ein Jahr hinterlegt, so wird uns die Bank am Ende des Jahres die Zinsen auf das Kapital unserem Konto gutschreiben. Für das Folgejahr haben wir nun aber nicht nur den ursprünglichen Betrag auf dem Konto, sondern den um die Zinsen des Vorjahres erhöhten Betrag. Und dieser erhöhte Betrag wird jetzt weiter verzinst, also zum einen das Eingangskapital und zum anderen die Zinsen; die verdienten Zinsen werden also auch verzinst. Deshalb sprechen wir von Zinseszinsen. |
Zinseszinsrechnung per Tabelle
| Was dies praktisch bedeutet, schauen wir uns an nachfolgender Tabelle an. Die Tabelle zeigt ein Anfangskapital von K0=1000 €, welches sich mit p%=3 % über einen Zeitraum von n=8 Jahren mit Zinsen verzinst. | ||||||
| Jahr | Kapital zu Jahresbeginn |
Zinssatz | Zinsen | Kapital am Jahresende |
||
| 1 | 1000,00 € | 3 % | 30,00 € | 1030,00 € | ||
| 2 | 1030,00 € | 3 % | 30,90 € | 1060,90 € | ||
| 3 | 1060,90 € | 3 % | 31,83 € | 1092,73 € | ||
| 4 | 1092,73 € | 3 % | 32,78 € | 1125,51 € | ||
| 5 | 1125,51 € | 3 % | 33,76 € | 1159,27 € | ||
| 6 | 1159,27 € | 3 % | 34,78 € | 1194,05 € | ||
| 7 | 1194,05 € | 3 % | 35,82 € | 1229,87 € | ||
| 8 | 1299,87 € | 3 % | 38,99 € | 1266,77 € | ||
| Aus einem Anfangskapital von K0=1000 € ist somit ein Endkapitel von K8=1266,78 € entstanden. Ohne den Zinseszinseffekt hätten wir pro Jahr ja nur 30,00 € zuschlagen dürfen, was bei n=8 Jahren dann zu einem Endkapital von nur K8=1240,00 € geführt hätte. Der Vorteil der Zinseszinsrechnung gegenüber der reinen Zinsrechnung beträgt in diesem Beispiel somit 26,77 €. | ||||||
Zinseszinsrechnung per Formel
| Jetzt haben wir schon einige Formelzeichen kennengelernt, nämlich K0, Kn, p % und n. Diese Zeichen stehen für: | |
| K0 = | Anfangskapital |
| Dies ist der Geldbetrag, den wir zur Bank bringen und anlegen, es ist aber auch gleichzeitig der Geldbetrag, den wir bei einer Bank ausleihen, weil wir einen Kredit benötigen. | |
| Kn = | Endkapital |
| Dies ist der Geldbetrag, den wir nach n Jahren auf unserem Konto zur Verfügung haben, wenn unser Anfangskapital n Jahre lang mit p % Zinsen verzinst wurde. | |
| p% = | Zinssatz |
| Dies ist der Prozentsatz, mit dem unser Anfangskapital Jahr für Jahr einschließlich Zinsen verzinst wird. | |
| n = | Anzahl der Jahre |
| Dies sind die Anzahl Jahre, die wir das Geld auf der Bank lassen zum verzinsen. | |
| Und diese vier Variablen bilden zusammen die Zinseszinsformel | |
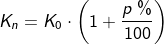 . . |
|
| Um jedoch nicht zu viel schreiben zu müssen – wir wissen ja, dass Mathematiker faule Leute sind -, wurde noch ein weiteres Zeichen q eingeführt mit dem Namen „Zinsfaktor“. Dieses q steht für | |
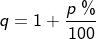 , , |
|
| sodass sich die Zinseszinsformel reduziert zu: | |
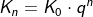 . . |
|
| Wir prüfen diese Formel gegen unsere Tabelle, die wir eingangs aufgestellt haben und berechnen das Endkapital Jahr für Jahr bei einem Anfangskapital von K0=1000 € und einem Zinssatz von p %=3 %: | |||||||
| Jahr | qn | Kn | Jahr | qn | Kn | ||
| 1 | 1,03 | 1030,00 € |
5 | 1,035 | 1159,27 € | ||
| 2 | 1,032 | 1060,90 € | 6 | 1,036 | 1194,05 € | ||
| 3 | 1,033 | 1092,73 € | 7 | 1,037 | 1229,87 € | ||
| 4 | 1,034 | 1125,51 € | 8 | 1,038 | 1266,77 € | ||
| Weitere Details zu Variationen der Zinseszinsformel findets du in den einzelnen Kapiteln „Kapitalentwicklung“, „Ratensparen“, „Darlehen“ und „Rentenrechnung“. | |||||||



