 |
WIKI zum Prozentwert der Prozentrechnung
|
Einleitung
| In der Prozentrechnung unterscheidet man drei Begriffe. Es sind dies: | |
| Der | Grundwert |
| Der Grundwert (auch Basiswert genannt) stellt stets die 100%-Basis der Prozentrechnung dar. Er ist der Basiswert für die Errechnung des Prozentwertes bzw. des Prozentsatzes. | |
| Der | Prozentwert |
| Der Prozentwert ist der Wert, der sich aus der Multiplikation des Grundwertes mit dem Prozentsatz ergibt. | |
| Der | Prozentsatz |
| Der Prozentsatz ist eine Dezimalzahl in %-Schreibweise, die angibt, wie viele Teile des Grundwertes den Prozentwert ergeben. In Prozentrechnungsaufgaben sind immer 2 der angeführten Variablen vorgegeben und die dritte Variable soll errechnet werden. Somit gibt es nur drei Arten von Prozentrechnungsaufgaben und zwar: |
|
Merksatz Prozentwert, Grundwert, Prozentsatz
| Gegeben Grundwert und Prozentsatz | ⇒ gesucht: Prozentwert | ||
| Gegeben Prozentwert und Prozentsatz | ⇒ gesucht: Grundwert | ||
| Gegeben Grundwert und Prozentwert | ⇒ gesucht: Prozentsatz | ||
| Es gibt keine anderen Arten von Aufgaben in der Prozentrechnung als diese drei aufgeführten Arten. | |||
| Je nach Schulart wird die Lösung solcher Aufgaben über die Dreisatzrechnung gelehrt bzw. auf eine viel einfachere Art und Weise, über Formeln. In diesem Kapitel behandeln wir die Lösung über die Formeln. Dazu müssen wir uns lediglich die nachfolgende Grafik sorgsam einprägen und schon können wir alle Prozentrechnungsaufgaben in Sekundenschnelle lösen. |
 |
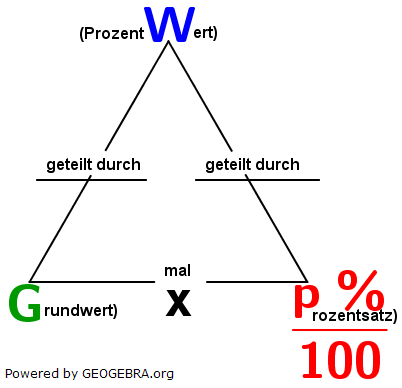| In der Grafik steht das W für den Prozentwert. Je nach Schultyp wird diese Variable auch mit dem Buchstaben P abgekürzt. Wird bei dir in der Schule dieses P benutzt, so betrachte in den folgenden Ausführungen stets das W als P. Das G steht für den Grundwert und das p % für den Prozentsatz. Die zwei waagrechten Striche im Dreieck stellen einen Bruchstrich dar. Ein Bruchstrich ist ja dasselbe wie ein : - Kennzeichen (geteilt durch). Aus der Grafik können wir nun ohne große Überlegung sofort die Rechenoperation ablesen, die wir zur Lösung einer Aufgabe anwenden müssen. |
Der Prozentwert
 |
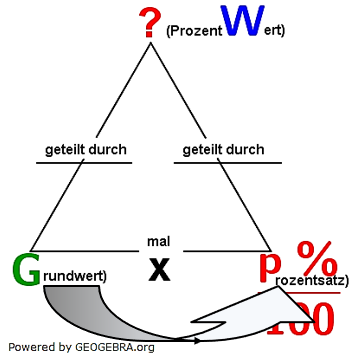Eine Aufgabe fragt nach dem ProzentWert. Den erhalten wir ganz einfach, indem wir den Grundwert mit dem  multiplizieren. Wir müssen lediglich beachten, dass wir den p %rozentsatz als Prozentzahl einsetzen müssen.Liegt der Prozentsatz bereits als Dezimalzahl ohne Prozentzeichen vor, müssen wir den Nenner mit „geteilt durch 100“ weglassen. |
Beispiel 1
| Was sind 20 % von 150 € ? |
Lösung 1
Beispiel 2
| Herr Maier darf von einer Lieferantenrechnung über 1500 € Skonto in Höhe von 3 % abziehen, wenn er innerhalb von 14 Tagen bezahlt. Welchen Betrag spart Herr Maier ein und welchen Bertag muss er noch bezahlen? |
Lösung 2
| Es gibt ein paar häufig vorkommende Prozentsätze, bei denen man den zugehörigen Prozentwert praktisch im Kopf ausrechnen kann. Diese findest du in nachfolgender Tabelle. | |
| Prozentsatz | Prozentwert = |
| 10 % | Teile den Grundwert durch 10. |
| 12,5 % | Teile den Grundwert durch 8. |
| 20 % | Teile den Grundwert durch 5. |
| 25 % | Teile den Grundwert durch 4. |
 |
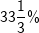Teile den Grundwert durch 3. |
| 50 % | Teile den Grundwert durch 2. |
 |
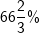Teile den Grundwert durch 3 und multipliziere diesen Wert mit 2. |
| 75 % | Teile den Grundwert durch 4 und multipliziere diesen Wert mit 3. |
| 100 % | Grundwert |
Der Prozentwert als vermehrter bzw. verminderter Grundwert
| Sehr häufig finden wir Prozentrechnungsaufgaben, bei denen nach einem „erhöhten Grundwert“ bzw. „verminderten Grundwert“ gefragt wird. Lassen wir uns durch diesen Ausdruck nicht verwirren. Auch der „erhöhte Grundwert“ bzw. „verminderte Grundwert“ ist nichts anderes als ein Prozentwert. Bei einer Aufgabe mit „erhöhtem Grundwert“ müssen wir nur zum angegebenen Prozentsatz 100 % addieren, also 100 % + Prozentsatz bilden. Beim „verminderten Grundwert“ müssen wir den angegebenen Prozentsatz von 100 % abziehen, also 100 % - Prozentsatz bilden. In nachfolgender Tabelle findest du einige gleichbedeutende Aufgaben-formulierungen gegenübergestellt, an Hand derer du erkennen kannst ob der echte Prozentwert oder aber der erhöhte bzw. verminderte Grundwert gemein ist. |
||
| Vergrößere 435 kg um 23 % |
Vergrößere 435 kg auf 123 % |
Berechne 123 % von 435 kg |
| Vermehre 78 € um 33 % |
Vermehre 78 € auf 133 % |
Berechne 133 % von 78 € |
| Vermindere 526 € um 14 % |
Vermindere 526 € auf 86 % |
Berechne 86 % von 526 € |
| Verringere 875 kg um 8,5 % |
Verringere 875 kg auf 91,5 % |
Berechne 91,5 % von 875 kg |
| Achte bei den Formulierungen auf Folgendes: | ||
| Steht in der Aufgabe auf bzw. von, so müssen wir mit dem angegebenen Prozentsatz rechnen. | ||
| Steht hingegen um, so müssen wir bei „vergrößere/vermehre“ | ||
| 100 % + Prozentsatz bilden, | ||
| wenn es heißt „vermindere/verringere“ | ||
| 100 % - Prozentsatz bilden. | ||
Beispiel 3
| Erhöhe einen Preis 150 € um 20 %. |
Lösung 3
Beispiel 4
| Ein Angestellter mit 2 410 € Monatsgehalt erhält eine Gehaltserhöhung von 4 %. Welches neue Gehalt erhält er? |
Lösung 4
Beispiel 5
 „Alles muss raus, 40 % Rabatt wegen Geschäftsaufgabe“ steht groß im Schaufenster von Manuelas Modeboutique zur lesen. Karin interessiert sich für ein Kleid, möchte vorher aber prüfen, ob der versprochene Nachlass auch richtig berechnet wurde. Auf einem Kleid findet sie das Schild mit dem Originalpreis 168,50 €. Mit welchem Preis müsste das Kleid bei 40 % Nachlass ausgezeichnet sein? |
Lösung 5
Prozentwert in der Prozentrechnung Aufgabenblatt Level 1 / Blatt 1  75 Aufgaben im Blatt |
| Prozentwert in der Prozentrechnung Aufgabenblatt Level 1 / Blatt 2 45 Aufgaben im Blatt |
| Prozentwert in der Prozentrechnung Aufgabenblatt Level 2 / Blatt 1 24 Aufgaben im Blatt |
| Prozentwert in der Prozentrechnung Aufgabenblatt Level 2 / Blatt 2 16 Aufgaben im Blatt |
| Prozentwert in der Prozentrechnung Aufgabenblatt Level 2 / Blatt 3 17 Aufgaben im Blatt |
