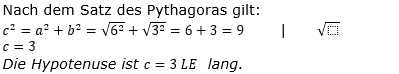 |
RS-Abschluss | Pflichtteil A1 nach Prüfungsjahr Mustersatz 4
|
Aufgabe A1/M4
| Berechne im Dreieck ABC die Länge der Hypotenuse c. |  |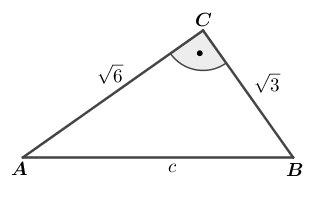
| Lösung: c=3 LE |
 Eine Frage stellen... |
Lösung A1/M4
Aufgabe A2/M4
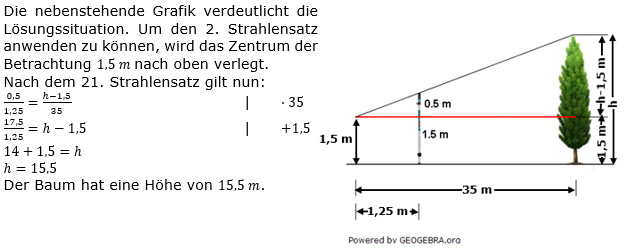
| Die Spitze eines Baums wird aus einer Höhe von 1,5 m über eine 2 m hohe Messlatte anvisiert. Berechne die Höhe des Baums. |
 |
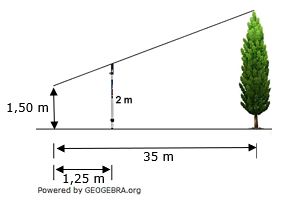| Lösung: hBaum=15,5 m |
| Eine Frage stellen... |
Lösung A2/M4
Aufgabe A3/M4
| Ein Metallwürfel mit einer Kantenlänge von a=4 cm wird in einer mit Wasser gefüllten quadratischen Säule vollständig versenkt (sieh Abb. rechts). Berechne, wie hoch dann das Wasser in der Säule steht. |
 |
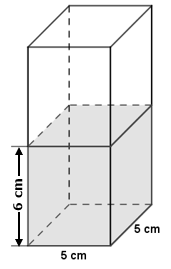| Lösung: hWasser=8,56 cm |
| Eine Frage stellen... |
Lösung A3/M4
Aufgabe A4/M4
| Zwei ideale Würfel werden gleichzeitig geworfen. | |
| a) | Bestimme die Wahrscheinlichkeit dafür, dass zwei verschiedene Augenzahlen fallen. |
| b) | Mit welcher Wahrscheinlichkeit erhält man eine „1“ und eine „2“? |
Lösung: P(2 verschiedene Augenzahlen)=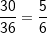 .P(„1“ und „2“)  . |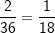
|
| Eine Frage stellen... |
Lösung A4/M4
Aufgabe A5/M4
| Begründe mithilfe eines Einheitskreises, dass gilt: sin(45 °)=cos(45 °) |
 |
| Eine Frage stellen... |
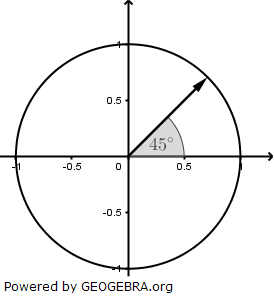Lösung A5/M4
Aufgabe A6/M4
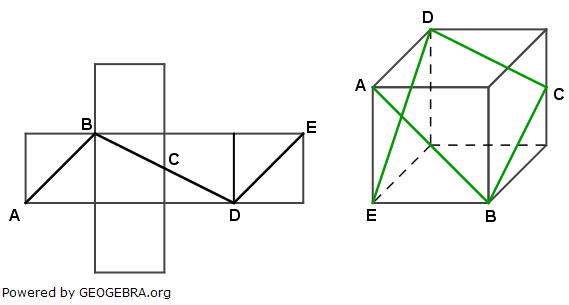
| Übertrage den in dem Würfelnetz markierten Streckenzug ABCDE in das Schrägbild des Würfels. Der Punkt C halbiert eine Würfelkante. |
 |
| Eine Frage stellen... |
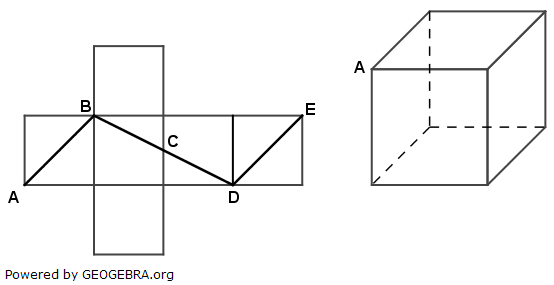Lösung A6/M4
Aufgabe A7/M4
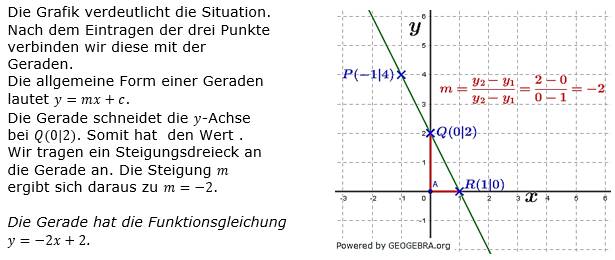
| Die Wertetabelle enthält drei Wertepaare einer Geraden. | x | -1 | 0 | 1 |
| Zeichne die Gerade in ein Koordinatensystem. | y | 4 | 2 | 0 |
| Lies daran die Gleichung der Geraden ab. | Lösung: y=-2x+2 | |||
| Eine Frage stellen... |
Lösung A7/M4
| Du befindest dich hier: |
| RS-Abschluss | Pflichtteil A1 nach Prüfungsjahr Mustersatz 4 |
