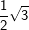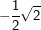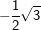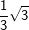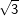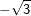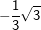|
Besondere Pyramiden Realschulabschluss |
Realschulabschluss Besondere Pyramiden | Themenerläuterung
(linke Maustaste zum Schließen/Öffnen)
| Ähnlich dem Kapitel „Quadratische Pyramiden“ geht es im Kapitel Besondere Pyramiden Realschulabschluss um regelmäßige Pyramiden mit anderen Grundflächen als einem Quadrat. Es kommen dreiseitige, fünfseitige, sechsseitige und achtseitige Pyramiden vor. Die Aufgabenstellung entspricht der aus Kapitel „Quadratische Pyramiden“. |
Die wichtigsten benötigten Formeln
(linke Maustaste zum Schließen/Öffnen)
1. Der Satz des Pythagoras
| Ist im rechtwinkligen Dreieck c die Hypothenuse (= längste Seite) und a und b die beiden Katheten, so gilt: |
c2=a2+b2 bzw. 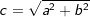 |
a2=c2-b2 bzw. 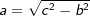 |
b2=c2-a2 bzw. 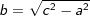 |
2. Die trigonometrischen Formeln
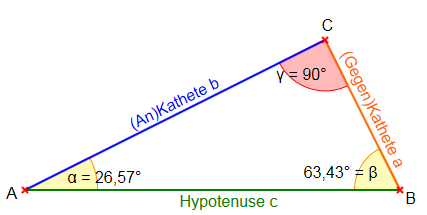 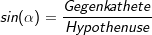 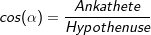 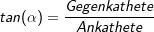 Die Hypothenuse ist immer die längste Seite im rechtwinkligen Dreieck und liegt dem rechten Winkel gegenüber. Die Gegenkathete ist die Kathete, die dem Winkel, um den es geht, gegenüber liegt. Die Ankathete ist die Kathete, die an dem Winkel, um den es geht, anliegt. |
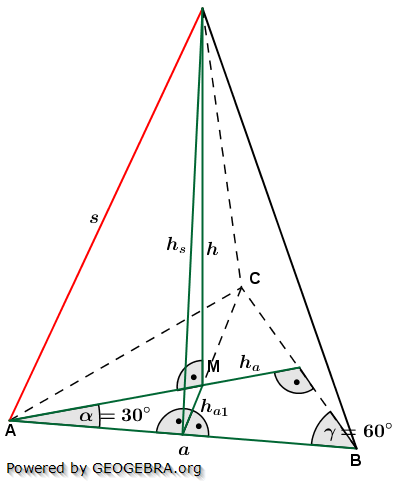
3. Regelmäßige Dreieckpyramide
3.1 Volumen, Oberfläche, Mantel
3.2 Höhe h
3.3 Höhe hS
3.4 Kante s
|
4. Regelmäßige Sechseckpyramide
4.1 Volumen, Oberfläche, Mantel
4.2 Höhe h
4.3 Höhe hS
4.4 Kante s
|
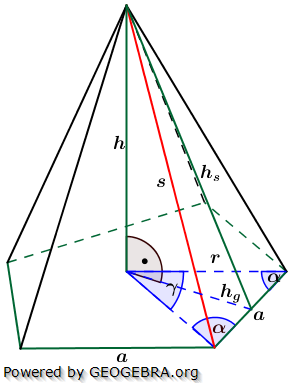
5. Regelmäßige n-Eckpyramide
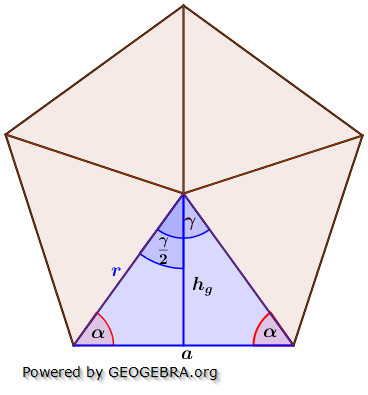 Die nachfolgenden Regeln und Formeln werden beispielhaft an einer 5-Eckpyramide erläutert. Grundlage der Betrachtung ist dabei die Grundfläche, die ja aus einem regelmäßigen n-Eck besteht. Die nachfolgenden Regeln und Formeln werden beispielhaft an einer 5-Eckpyramide erläutert. Grundlage der Betrachtung ist dabei die Grundfläche, die ja aus einem regelmäßigen n-Eck besteht. Wie du aus der Grafik erkennst, ist die Grundfläche des n-Ecks in n kongruente Dreiecke unterteilt. Diese Dreiecke sind gleichschenklig, das heißt, a ist die Grundeite und r sind die beiden gleich langen Schenkel jeden Dreiecks. hg ist die Höhe dieser n Dreiecke. γ ist der Spitzenwinkel und α ist der Basiswinkel. Wenn du nun die n Spitzenwinkel zusammenzählst, müssen ja 360° herauskommen, denn einmal um die Mittelpunkt herum entspricht ja 360°. Aus dieser Gesetzmäßigkeit heraus kannst du in jeder n–Eckaufgabe sofort die Größe der Winkel α und γ bestimmen, denn es gilt: 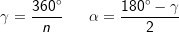 Hast du die Winkel bestimmt, steht der Berechnung der Seitenlänge r sowie der Grundflächendreieckshöhe hg nichts mehr im Wege.
5.1 Volumen, Oberfläche, Mantel
5.2 Höhe h
5.3 Höhe hS
5.4 Kante s
|
||||||||||||||||||||||||||||||||||||||||||
6. Besondere Werte für sin, cos und tan
Einige Aufgaben sind in Abhängigkeit einer sogenannten „Formvariablen“ gestellt. Diese Formvariable wird mit dem Buchstaben "e" bezeichnet. In diesen Aufgaben wird verlangt, dass du den Nachweis ohne gerundete Werte führen sollst. Dies bedeutet für dich, dass du keinen Taschenrechner verwenden kannst und die Aufgabe manuell lösen musst. In diesen Aufgaben handelt es sich stets nur um Winkel der Größe 30°, 45°, 60° bzw. 90°. Für diese Winkelgrößen gibt es besondere Werte, die in nachstehender Tabelle aufgeführt sind. Diese Tabelle findest du auch in deiner Formelsammlung.
|
| Aufgaben nach Aufgabengebiet Übungen / Pflicht- / Wahlteile |

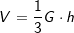 mit
mit 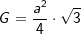 (Fläche eines gleichseitigen Dreiecks), a ist Seitenkante der Grundfläche, h ist die Höhe der Pyramide.
(Fläche eines gleichseitigen Dreiecks), a ist Seitenkante der Grundfläche, h ist die Höhe der Pyramide. 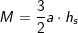 , a ist Seitenkante der Grundfläche, hs ist die Höhe eines Seitendreiecks.
, a ist Seitenkante der Grundfläche, hs ist die Höhe eines Seitendreiecks. 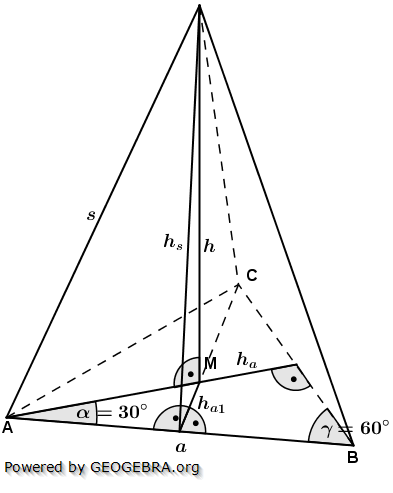
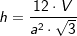 , a ist Seitenkante der Grundfläche.
, a ist Seitenkante der Grundfläche.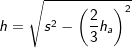 mit
mit 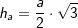 , a ist Seitenkante der Grundfläche.
, a ist Seitenkante der Grundfläche.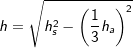 mit
mit 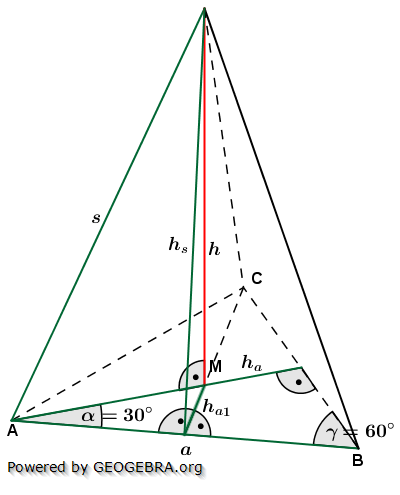
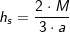 , a ist Seitenkante der Grundfläche.
, a ist Seitenkante der Grundfläche.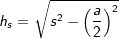 .
.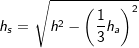 mit
mit 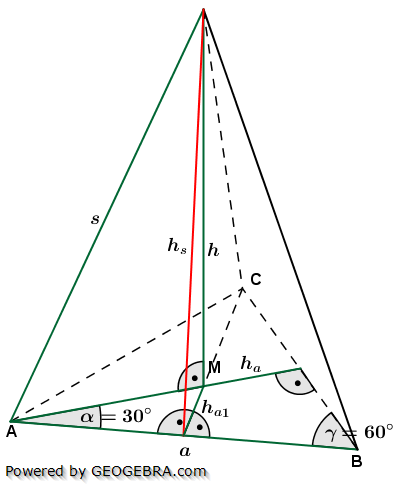
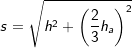 mit
mit 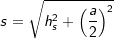 .
.
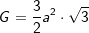 (Fläche eines regelmäßigen Sechsecks), somit
(Fläche eines regelmäßigen Sechsecks), somit 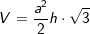 . a ist Seitenkante der Grundfläche, h ist die Höhe der Pyramide.
. a ist Seitenkante der Grundfläche, h ist die Höhe der Pyramide.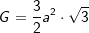 und M=3a⋅hs, a ist Seitenkante der Grundfläche, hs ist die Höhe eines Seitendreiecks.
und M=3a⋅hs, a ist Seitenkante der Grundfläche, hs ist die Höhe eines Seitendreiecks.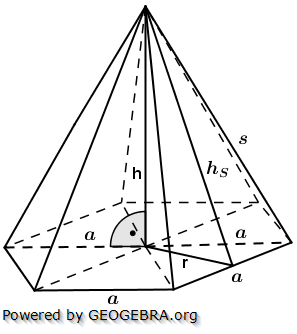
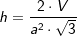 , a ist Seitenkante der Grundfläche.
, a ist Seitenkante der Grundfläche.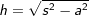 .
.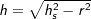 mit
mit 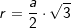 , a ist Seitenkante der Grundfläche.
, a ist Seitenkante der Grundfläche.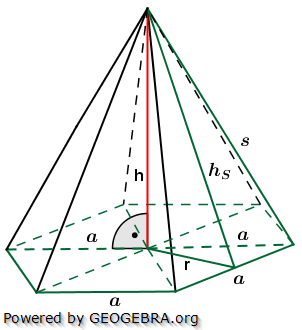
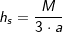 , a ist Seitenkante der Grundfläche.
, a ist Seitenkante der Grundfläche. .
.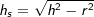 mit
mit 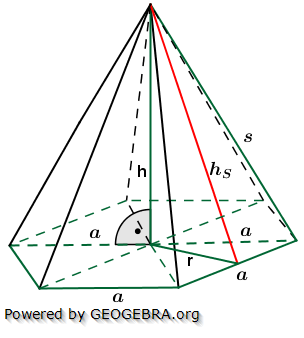
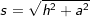 , a ist Seitenkante der Grundfläche.
, a ist Seitenkante der Grundfläche.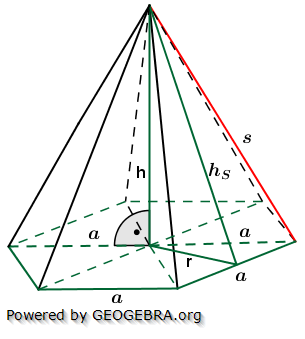
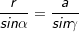 ⟹
⟹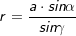
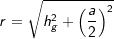
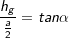 ⟹
⟹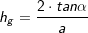
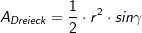
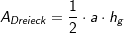
 bzw.
bzw. 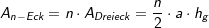 .
. Das Volumen einer regelmäßigen n-Eckpyramide errechnet sich aus
Das Volumen einer regelmäßigen n-Eckpyramide errechnet sich aus 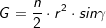 (Fläche eines regelmäßigen n-Ecks), somit:
(Fläche eines regelmäßigen n-Ecks), somit: 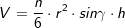 .
.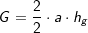 somit:
somit: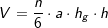 . a ist Seitenkante der Grundfläche, h ist die Höhe der Pyramide.
. a ist Seitenkante der Grundfläche, h ist die Höhe der Pyramide.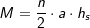 , a ist Seitenkante der Grundfläche, hs ist die Höhe eines Seitendreiecks.
, a ist Seitenkante der Grundfläche, hs ist die Höhe eines Seitendreiecks.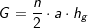 und
und 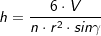 , alternativ
, alternativ 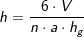 .
.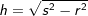 .
.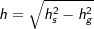 mit
mit 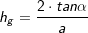 , a ist Seitenkante der Grundfläche.
, a ist Seitenkante der Grundfläche.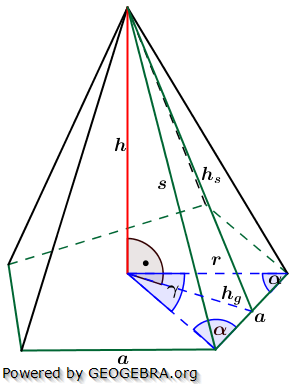
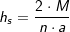 , a ist Seitenkante der Grundfläche.
, a ist Seitenkante der Grundfläche.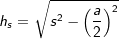 .
.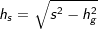 mit
mit 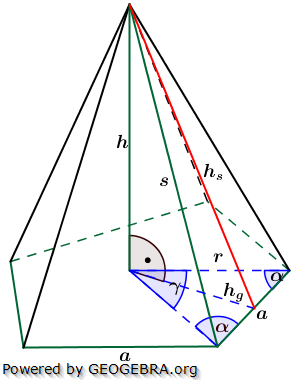
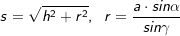 .
.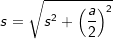 , a ist die Seitenkante der Grundfläche.
, a ist die Seitenkante der Grundfläche.