 |
Lineare Gleichungssysteme Realschulabschluss |

Lineare Gleichungssysteme - Themenerläuterung
(linke Maustaste zum Schließen/Öffnen)
| Das Thema Lineare Gleichungssyteme im Realschulabschluss verlangt von dir die Bestimmung der Lösungsmenge eines Gleichungsterms aus zwei Gleichungen mit den zwei Unbekannten x und y. Die beiden gestellten Terme musst du nach den Regeln der Äquivalenzumformung in die Form y=mx+b bringen. Dabei musst du vor allem die "PoKlaPS"-Regeln „Potenzrechnung vor Klammern“, „Klammern vor Punktrechnung“, „Punktrechnung vor Strichrechnung“ beachten. Es entstehen jedes Mal zwei Gleichungen, deren Lösungsmenge mit dem „Einsetzungs- “, „Gleichsetzungs-„ bzw. „Additions-(Subtraktions-)verfahren„ zu bestimmen ist. Ich empfehle dir, das „Additions- (Subtraktions-)verfahren“ zu verwenden, weil damit die wenigsten Fehler passieren. In diesen Dokumenten wird ausschließlich das „Additions-(Subtraktions-)verfahren“ verwendet. |
Die wichtigsten benötigten Formeln
(linke Maustaste zum Schließen/Öffnen)
| 1. | Kommutativgesetz (Vertauschen von Variablen) | |
| a+b=b+a | a⋅b=b⋅a | |
| 2. | Distributivgesetz (ausmultiplizieren) | |
| Faktor mal Klammer: | a⋅(b+c)=a⋅b+a⋅c | |
| Klammer mal Klammer: | (a+b)⋅(c+d)=a⋅c+a⋅d+b⋅c+b⋅d | |
| 3. | Assoziativgesetz (Verbindungsgesetz) | |
| a+(b+c)=(a+b)+c | a⋅(b⋅c)=a⋅(b⋅c) | |
| 4. | Addition / Subtraktion | |
| a+a+a=3a | -a-a-a=-3a | |
| 5. | Multiplikation / Division | |
| a⋅a=+a2 | a⋅(-a)=-a2 | (-a)⋅a=-a2 | (-a)⋅(-a)=+a2 | |
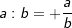 |
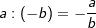 |
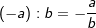 |
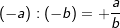 |
| Aufgaben nach Aufgabengebiet Übungen / Pflicht- / Wahlteile |



