 |
Bruchgleichungen Realschulabschluss |

Bruchgleichungen - Themenerläuterung
(linke Maustaste zum Schließen/Öffnen)
Das Thema „Bruchgleichungen“ verlangt von dir die Bestimmung der Lösungsmenge eines Gleichungsterms, in dem die Variable x auch im Nenner vorkommt. Als erstes musst du einen Hauptnenner aufstellen. Über diesen Hauptnenner legst du dann den Definitionsbereich 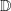 des Gleichungsterms fest. Danach musst du alle Elemente der Gleichung mit dem Hauptnenner multiplizieren und dann die einzelnen Elemente kürzen. Dies führt dazu, dass alle Nenner der Gleichung verschwinden. Du erhältst in der Regel eine quadratische Gleichung, die du dann nach x auflösen musst zur Berechnung der Lösungsmenge des Gleichungsterms fest. Danach musst du alle Elemente der Gleichung mit dem Hauptnenner multiplizieren und dann die einzelnen Elemente kürzen. Dies führt dazu, dass alle Nenner der Gleichung verschwinden. Du erhältst in der Regel eine quadratische Gleichung, die du dann nach x auflösen musst zur Berechnung der Lösungsmenge 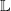 . .Die Auflösung nach erfolgt nach demselben Prinzip wie unter "Realschulabschluss Gleichungen" bereits geübt. |
Die wichtigsten benötigten Formeln
(linke Maustaste zum Schließen/Öffnen)
| 1. | Kommutativgesetz (Vertauschen von Variablen) | |
| a+b=b+a | a⋅b=b⋅a | |
| 2. | Distributivgesetz (ausmultiplizieren) | |
| Faktor mal Klammer: | a⋅(b+c)=a⋅b+a⋅c | |
| Klammer mal Klammer: | (a+b)⋅(c+d)=a⋅c+a⋅d+b⋅c+b⋅d | |
| 3. | Assoziativgesetz (Verbindungsgesetz) | |
| a+(b+c)=(a+b)+c | a⋅(b⋅c)=(a⋅b)⋅c | |
| 4. | Addition / Subtraktion | |
| a+a+a=3a | -a-a-a=-3a | |
| 5. | Multiplikation / Division | |
| a⋅a=+a2 | a⋅(-a)=-a2 | (-a)⋅a=-a2 | (-a)⋅(-a)=+a2 | |
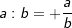 |
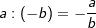 |
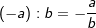 |
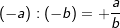 |
| 6. | 1. binomische Formel | (a+b)2=a2+2ab+b2 |
| 7. | 2. binomische Formel | (a-b)2=a2-2ab+b2 |
| 8. | 3. binomische Formel | (a+b)(a-b)=a2-b2 |
| und zusätzlich | ||
| 9. | Faktorisieren (ausklammern) | |
| 3x+9=3⋅(x+3) | ||
| 10. | Rückführung binomischer Ausdrücke in die binomischen Formeln wie beispielsweise | |
| 4x2+12x+9=(2x+3)2 | ||
| x2-12x+36=(x-6)2 | ||
| 4-x2=(2+x)⋅(2-x) | ||
| Aufgaben nach Aufgabengebiet Übungen / Pflicht- / Wahlteile |



