Pflichtteile Abitur allgemeinbildendes bildendes Gymnasium nach Prüfungsjahr/© by www.fit-in-mathe-online.de

2010 Abituraufgaben allg. Gymnasium Pflichtteil

Aufgaben des Prüfungsjahres 2010 BW

Aufgabe A1

Bilden Sie die Ableitung der Funktion f mit f(x)=(2-3x) ⋅ e^-x und vereinfachen Sie so weit wie möglich.

Lösung A1

Aufgabe A2

Berechnen Sie das Integral $Fit in Mathe Latex: 499903dbee28d0d1aa599eb120ea6c62.png$ .

Lösung A2

Aufgabe A3

Die Funktion f mit f(x)=2x³+3x²-8x+3 hat die Nullstelle x₁=1. Bestimmen Sie alle weiteren Nullstellen von f.

Lösung A3

Aufgabe A4

Das Schaubild der Funktion f mit 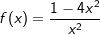$Fit in Mathe Latex: 7abd7b4f13f09d1a5555386bc5e456d2.png$ . Ihr Schaubild sei K.

a)	Geben Sie die Asymptoten von K an.
b)	Bestimmen Sie den Schnittpunkt der Tangente an K im Punkt P(1\|f(1)) mit der x–Achse.

Lösung A4

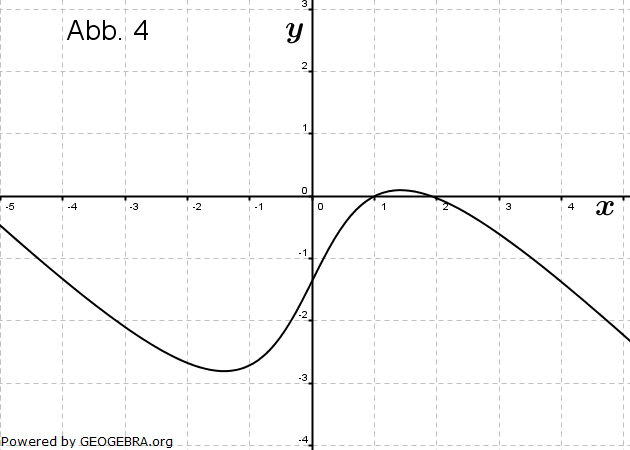
Aufgabe A5

Die Abbildungen zeigen Schaubilder von Funktionen einschließlich aller waagrechten Asymptoten.
Eines dieser Schaubilder gehört zur Funktion f mit $Fit in Mathe Latex: dcf827a187e14e0ddc917c257585a438.png$ .

Die Abbildungen zeigen Schaubilder von Funktionen einschließlich aller waagrechten Asymptoten. (Graphik zur Abituraufgabe allg. bildendes Gymnasium Pflichtteilaufgaben 'grafisches Differenzieren und Integrieren' 2010 Bild 1/© by www.fit-in-mathe-online.de)

a)	Begründen Sie, dass Abbildung 2 zur Funktion f gehört. Bestimmen Sie den Wert von a.
b)	Von den anderen drei Abbildungen gehört eine zur Ableitungsfunktion f' und eine zur Integralfunktion I mit $Fit in Mathe Latex: 39fe730b159b5ec355a3791edd84226b.png$ . Ordnen Sie diesen beiden Funktionen die zugehörigen Abbildungen zu und begründen Sie jeweils Ihre Entscheidung.

{snippet snippet-graphik-drucken}

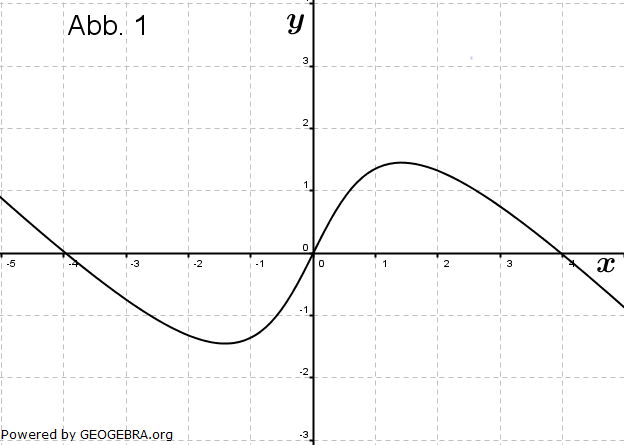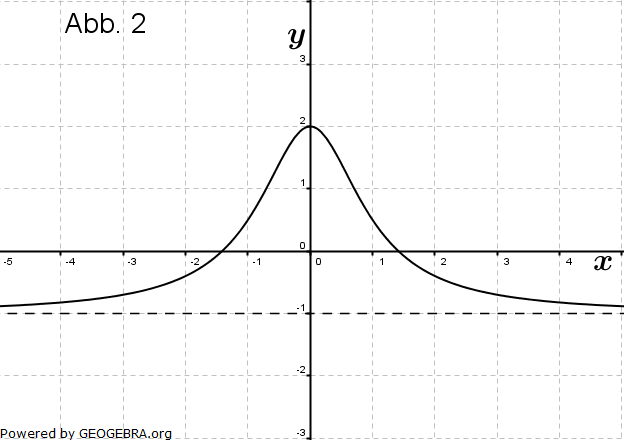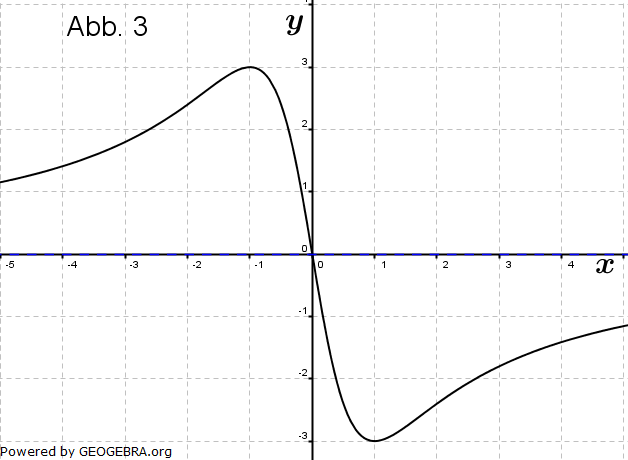
Lösung A5

Aufgabe A6

Gegeben sind die Punkte A(2|4|1), B(0|2|-1), C(4|-2|1) und D(-1|9|0).
Überprüfen Sie, ob diese vier Punkte in einer Ebene liegen.

Lösung A6

Aufgabe A7

Gegeben sind die Ebene E: 3x₁-4x₃=-7 und der Punkt P(9\|-4\|1).
a)	Berechnen Sie den Abstand des Punktes P von der Ebene E.
b)	Der Punkt S(-1\|1\|1) liegt auf E.
	Bestimmen Sie den Punkt Q auf der Geraden durch S und P, der genauso weit von E entfernt ist wie P.

Lösung A7

Aufgabe A8

Die Gerade g und die Ebene E schneiden sich im Punkt S.
Die Gerade g' ist das Bild von g bei Spiegelung an der Ebene E.
Beschreiben Sie ein Verfahren, um eine Gleichung der Geraden g' zu ermitteln.

Lösung A8

Du befindest dich hier:

2010 Abituraufgaben allg. Gymnasium Pflichtteil
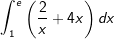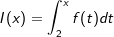