 |
Abituraufgaben allg. Gymnasium Pflichtteil Analysis
|
Aufgaben der Prüfungsjahre 2004 - 2018 BW |
| Dokument mit 17 Aufgaben |
Aufgabe A4/04
Gegeben ist die Funktion 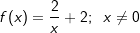 . .Das Schaubild von f hat im Punkt P(1|v) die Tangente t. Ermitteln Sie eine Gleichung von t. Die Tangente t schneidet die x–Achse im Punkt S. Bestimmen Sie die Koordinaten von S. |
| |
Lösung A4/04
Aufgabe A4/05
Gegeben ist die Funktion f mit 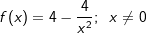 . .Geben Sie die Asymptoten des Schaubilds von f an. Skizzieren Sie damit das Schaubild von f. Ermitteln Sie eine Gleichung der Normalen im Punkt P(2|f(2)). |
| |
Lösung A4/05
Aufgabe A4/06
| Das Schaubild einer ganzrationalen Funktion dritten Grades berührt die x-Achse im Ursprung. Der Punkt H(1|1) ist der Hochpunkt des Schaubilds. Bestimmen Sie die Funktionsgleichung. |
| |
Lösung A4/06
Aufgabe A4/07
Gegeben ist die Funktion f mit 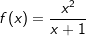 . .
|
| |
Lösung A4/07
Aufgabe A4/08
| Für eine ganzrationale Funktion h zweiten Grades gilt: T(-1|-4) ist der Tiefpunkt und Q(2|5) ein weiterer Punkt ihres Schaubilds. Ermitteln Sie eine Funktionsgleichung von h. |
| |
Lösung A4/08
Aufgabe A4/09
| Das Schaubild der Funktion f mit f(x)=-x3+3x2-x-3 besitzt einen Wendepunkt. Bestimmen Sie eine Gleichung der Tangente an diesen Wendepunkt. |
| |
Lösung A4/09
Aufgabe A4/10
Das Schaubild der Funktion f mit 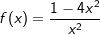 . Ihr Schaubild sei K. . Ihr Schaubild sei K.
|
| |
Lösung A4/10
Aufgabe A4/11
Gegeben sind die Funktionen f und g mit f(x)=ex und g(x)=-e-x+2.
|
| |
Lösung A4/11
Aufgabe A4/12
Gegeben sind die Funktionen f und g mit 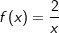 und g(x)=2x-3. und g(x)=2x-3.Bestimmen Sie die gemeinsamen Punkte der beiden zugehörigen Graphen. Untersuchen Sie, ob sich die beiden Graphe senkrecht schneiden. |
| |
Lösung A4/12
Aufgabe A4/13
| Gegeben sind die Funktionen f und g mit f(x)=-x2+6 und g(x)=2x. Berechnen Sie den Inhalt der Fläche, die von den Graphen der beiden Funktionen eingeschlossen wird. |
| |
Lösung A4/13
Aufgabe A9/13
| Gibt es eine ganzrationale Funktion vierten Grades, deren Graph drei Wendepunkte besitzt? Begründen Sie Ihre Antwort. |
| |
Lösung A9/13
Aufgabe A4/14
Gegeben sind die Funktionen f und g mit f(x)=cos(x) und 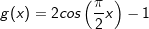 . .
|
| |
Lösung A4/14
Aufgabe A4/15
| Der Graph einer ganzrationalen Funktionen f dritten Grades hat im Ursprung einen Hochpunkt und an der Stelle x=2 die Tangente mit der Gleichung y=4x-12. Bestimmen Sie eine Funktionsgleichung von f. |
| |
Lösung A4/15
Aufgabe A9/15
Mit 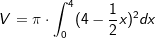 wird der Rauminhalt eines Körpers berechnet. wird der Rauminhalt eines Körpers berechnet.Skizzieren Sie diesen Sachverhalt und beschreiben Sie den Körper. |
| |
Lösung A9/15
Aufgabe A4/16
Der Graph der Funktionen f mit 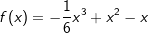 besitzt einen Wendepunkt. besitzt einen Wendepunkt.Zeigen Sie, dass 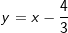 eine Gleichung der Tangente in diesem Wendepunkt ist. eine Gleichung der Tangente in diesem Wendepunkt ist. |
| |
Lösung A4/16
Aufgabe A4/17
Sind die folgenden Aussagen wahr? Begründen Sie jeweils Ihre Entscheidung.
|
| |
Lösung A4/17
Aufgabe A3/18
| Gegeben ist die Funktion f mit f(x)=4x2-4x+5. F ist eine Stammfunktion von f. Bestimmen Sie die Stelle, an der die Graphen von F und f parallele Tangenten besitzen. |
| |
Lösung A3/18
| Du befindest dich hier: |
| Abituraufgaben allg. Gymnasium Pflichtteil Analysis |




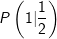 die Normale n. Ermitteln Sie die Gleichung von n.
die Normale n. Ermitteln Sie die Gleichung von n.

