Pflichtteilaufgaben Abitur allgemeinbildendes bildendes Gymnasium zur Analytischen Geometrie/© by www.fit-in-mathe-online.de

Abituraufgaben allg. Gymnasium Pflichtteil Analytische Geometrie I

Aufgaben der Prüfungsjahre 2004 - 2007 BW

Dokument mit 12 Aufgaben

Aufgabe 6/04

Gegeben sind die Gerade g und die Ebene E durch
	$Fit in Mathe Latex: 9b48aa4dcff215cbcb8ad7ac8e1891dd.png$
	E: 4x₁-2x₂+4x₃=11.
Prüfen Sie nach, ob der Punkt A(3\|0\|2) auf der Geraden g liegt. Zeigen Sie: Die Gerade g ist orthogonal zur Ebene E. Bestimmen Sie die Koordinaten desjenigen Punktes der Ebene E, welcher vom Punkt A den kleinsten Abstand hat.

(Quelle Abitur BW 2004 Aufgabe 6)

Lösung A6/04

Aufgabe 7/04

Ermitteln Sie eine Koordinatengleichung der dargestellten Ebene.

(Quelle Abitur BW 2004 Aufgabe 7)

Lösung A7/04

Aufgabe 8/04

Gegeben sind im Raum eine Gerade g und ein Punkt A, der nicht auf g liegt.
Beschreiben Sie ein Verfahren zur Bestimmung des Abstandes von A zu g.

(Quelle Abitur BW 2004 Aufgabe 8)

Lösung A8/04

Aufgabe 6/05

Lösen Sie das lineare Gleichungssystem
	x₁+4x₂+x₃=10
	x₁+2x₂+x₃=8
	x₁+ x₂-x₃=3
Wie lässt sich ein solches Gleichungssystem und seine eindeutige Lösung geometrisch deuten?

(Quelle Abitur BW 2005 Aufgabe 6)

Lösung A6/05

Aufgabe 7/05

Ermitteln Sie eine Koordinatengleichung der Ebene, die den Punkt A(2|-1|-2) und die Gerade 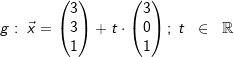$Fit in Mathe Latex: de76369ffa9f6ff12ae286367406c99e.png$ enthält.

(Quelle Abitur BW 2005 Aufgabe 7)

Lösung A7/05

Aufgabe 8/05

Gegeben sind die Ebene E und ein Punkt P, der nicht auf E liegt. P wird an E gespiegelt.
Beschreiben Sie ein Verfahren, um den Bildpunkt P' zu bestimmen. Fertigen Sie eine Skizze an.

(Quelle Abitur BW 2005 Aufgabe 8)

Lösung A8/05

Aufgabe 6/06

Gegeben sind die Ebene
	E: -2x₁+x₂-2x₃+15=0 und die Gerade
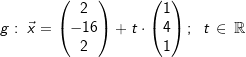	$Fit in Mathe Latex: 32a94309d9eadcbdf0a4ffe599bdf076.png$ .
a)	Zeigen Sie, dass E zu g parallel ist.
b)	Bestimmen Sie den Abstand der Geraden g von der Ebene E.

(Quelle Abitur BW 2006 Aufgabe 6)

Lösung A6/06

Aufgabe 7/06

Gegeben sind die Ebenen E₁ und E₂ mit
	E₁: 4x₁+3x₂+2x₃=12
	E₂: 3x₁+2x₂=6
Stellen Sie die beiden Ebenen in einem Koordinatensystem dar. Zeichnen Sie die Schnittgerade der beiden Ebenen ohne weitere Rechnung ein.

(Quelle Abitur BW 2006 Aufgabe 7)

Lösung A7/06

Aufgabe 8/06

Gegeben sind zwei Punkte A und B. Diese liegen bezüglich einer Ebene E symmetrisch.
Beschreiben Sie ein Verfahren zur Bestimmung einer Gleichung von E.

(Quelle Abitur BW 2006 Aufgabe 8)

Lösung A8/06

Aufgabe 6/07

Lösen Sie das lineare Gleichungssystem:
	3x₁- x₂+2x₃=7
	x₁+2x₂+3x₃=14
	x₁-5x₂-4x₃=-21
Interpretieren Sie das Gleichungssystem und seine Lösungsmenge geometrisch.

(Quelle Abitur BW 2007 Aufgabe 6)

Lösung A6/07

Aufgabe 7/07

Gegeben sind die Ebenen E und F mit
	$Fit in Mathe Latex: 85f6e474ff562bb543b1c6985e2f4cb7.png$
	$Fit in Mathe Latex: 4bcb0e085c7fe5f25e0635ee5bbfc778.png$
Zeigen Sie, dass die Ebenen E und F parallel sind. Bestimmen Sie den Abstand der Ebenen.

(Quelle Abitur BW 2007 Aufgabe 7)

Lösung A7/07

Aufgabe 8/07

Von einem senkrechten Kegel kennt man die Koordinaten der Spitze S, die Koordinaten eines Punktes P des Grundkreises sowie eine Koordinatengleichung der Ebene E, in der der Grundkreis liegt.
Beschreiben Sie ein Verfahren, um den Mittelpunkt M und den Radius r des Grundkreises zu bestimmen.

(Quelle Abitur BW 2007 Aufgabe 8)

Lösung A8/07

Du befindest dich hier:

Abituraufgaben allg. Gymnasium Pflichtteil Analytische Geometrie I