Pflichtteilaufgaben Abitur allgemeinbildendes bildendes Gymnasium zur Analytischen Geometrie/© by www.fit-in-mathe-online.de

Abituraufgaben allg. Gymnasium Pflichtteil Analytische Geometrie II

Aufgaben der Prüfungsjahre 2008 - 2011 BW

Dokument mit 12 Aufgaben

Aufgabe 6/08

Gegeben sind die zwei parallelen Geraden g und h durch
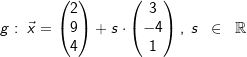	$Fit in Mathe Latex: fe346d5a8d97568707192fea45483ed5.png$
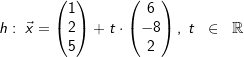	$Fit in Mathe Latex: b6bc699cd19ec01f03ff21acec3858d5.png$
Bestimmen Sie den Abstand der beiden Geraden.

(Quelle Abitur BW 2008 Aufgabe 6)

Lösung 6/08

Lösung 6/08 umständlich

Aufgabe 7/08

Die Ebene E geht durch die Punkte A(1,5|0|0), B(0|3|0) und C(0|0|6). Untersuchen Sie, ob die Gerade 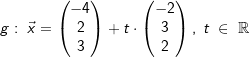$Fit in Mathe Latex: 0beb51b07a361e98a2a11e170e636e14.png$ parallel zur Ebene E verläuft.

(Quelle Abitur BW 2008 Aufgabe 7)

Lösungen 7/08

Aufgabe 8/08

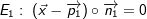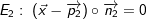Gegeben sind die beiden Ebenen $Fit in Mathe Latex: 8e054fbd5a5037c61ca90483b07c3631.png$ und $Fit in Mathe Latex: 742eb62b88d6a4d1d5e95b01c354f369.png$ . Beschrieben Sie ein Verfahren, mit dem man anhand dieser Normalengleichungen die gegenseitige Lage der beiden Ebenen untersuchen kann.

(Quelle Abitur BW 2008 Aufgabe 8)

Lösungen 8/08

Aufgabe 6/09

Untersuchen Sie, ob die Vektoren 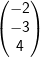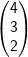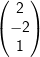$Fit in Mathe Latex: 619d5851ff868b5e2a664c11dc5045bb.png$ , $Fit in Mathe Latex: 0deaf6289d123365266aa4e904a5ac3a.png$ , $Fit in Mathe Latex: 73451770846bbc898b8394210ddf151a.png$ linear unabhängig sind.

(Quelle Abitur BW 2009 Aufgabe 6)

Lösung 6/09

Lösung 6/09 umständlich

Aufgabe 7/09

Gegeben sind die Ebene E: x₁+x₂=4 und die Gerade
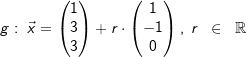	$Fit in Mathe Latex: b44c5710e488d51df1d88f848e5195c0.png$ .
a)	Veranschaulichen Sie die Ebene E in einem Koordinatensystem.
b)	Untersuchen Sie die gegenseitige Lage von g und E.
c)	Bestimmen Sie den Abstand des Ursprungs von der Ebene E.

(Quelle Abitur BW 2009 Aufgabe 7)

Lösungen 7/09

Aufgabe 8/09

Gegeben sind eine Gerade g und ein Punkt A im Raum. A liegt nicht auf g.
A wird an der Geraden g gespiegelt.
Beschreiben Sie ein Verfahren, um den Bildpunkt A' zu bestimmen.

(Quelle Abitur BW 2008 Aufgabe 9)

Lösungen 8/09

Aufgabe 6/10

Gegeben sind die Punkte A(2|4|1), B(0|2|-1), C(4|-2|1) und D(-1|9|0).
Überprüfen Sie, ob diese vier Punkte in einer Ebene liegen.

(Quelle Abitur BW 2010 Aufgabe 6)

Lösung 6/10

Lösung 6/10 umständlich

Aufgabe 7/10

Gegeben sind die Ebene E: 3x₁-4x₃=-7 und der Punkt P(9\|-4\|1).
a)	Berechnen Sie den Abstand des Punktes P von der Ebene E.
b)	Der Punkt S(-1\|1\|1) liegt auf E.
	Bestimmen Sie den Punkt Q auf der Geraden durch S und P, der genauso weit von E entfernt ist wie P.

(Quelle Abitur BW 2010 Aufgabe 2)

Lösungen 7/10

Aufgabe 8/10

Die Gerade g und die Ebene E schneiden sich im Punkt S.
Die Gerade g' ist das Bild von g bei Spiegelung an der Ebene E.
Beschreiben Sie ein Verfahren, um eine Gleichung der Geraden g' zu ermitteln.

(Quelle Abitur BW 2010 Aufgabe 9)

Lösungen 8/10

Aufgabe 6/11

Lösen Sie das lineare Gleichungssystem;
	-5x₁+x₂-3x₃=7
	5x₁- 3x₂- x₃=-11
	x₁ +x₃=-1
Interpretiren Sie das Gleichungssystem und seine Lösungsmenge geometrisch.

(Quelle Abitur BW 2011 Aufgabe 6)

Lösungen 6/11

Aufgabe 7/11

Gegeben sind die Ebene
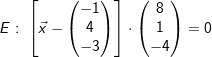	$Fit in Mathe Latex: f61a16ec4ed442d297e88089bf23876a.png$
und die Gerade
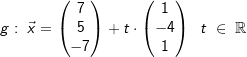	$Fit in Mathe Latex: 12f3e36fcfdf344f6355d66a41ad3208.png$ .
a)	Zeigen Sie, dass E und g parallel zueinander sind.
b)	Bestimmen Sie den Abstand E von g.

(Quelle Abitur BW 2011 Aufgabe 7)

Lösungen 7/11

Aufgabe 8/11

Gegeben sind eine Gerade g und ein Punkt A, der nicht auf g liegt. Beschreiben Sie ein Verfahren, mit dem man denjenigen Punkt B auf g bestimmt, der den kleinste Abstand von A hat.

(Quelle Abitur BW 2011 Aufgabe 9)

Lösungen 8/11

Du befindest dich hier:

Abituraufgaben allg. Gymnasium Pflichtteil Analytische Geometrie II