Pflichtteilaufgaben Abitur allgemeinbildendes bildendes Gymnasium zur Analytischen Geometrie/© by www.fit-in-mathe-online.de

Abituraufgaben allg. Gymnasium Pflichtteil Analytische Geometrie III

Aufgaben der Prüfungsjahre 2012 - 2018 BW

Dokument mit 17 Aufgaben

Aufgabe A6/12

Gegeben sind die Ebenen
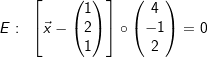	$Fit in Mathe Latex: 28035c123e0a5b141a80861d2196df41.png$
und
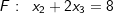	$Fit in Mathe Latex: eabdb17c77080fe8b31749fcfbd67ecf.png$ .
Bestimmen Sie eine Gleichung der Schnittgeraden.

(Quelle Abitur BW 2012 Aufgabe 6)

Lösung A6/12

Aufgabe A7/12

Gegeben sind die Punkte A(1\|1\|3) und die Ebene E: x₁-x₃-4=0.
a)	Welche besondere Lage hat E im Koordinatensystem?
b)	Der Punkt A wird an der Ebene E gespiegelt. Bestimmen Sie die Koordinaten des Bildpunktes.

(Quelle Abitur BW 2012 Aufgabe 7)

Lösung A7/12

Aufgabe A8/12

Gegeben sind eine Ebene E und ein Gerade g, die in E liegt. Beschreiben Sie ein Verfahren, mit dem man eine Gleichung einer Geraden h ermitteln kann, die orthogonal zu g ist und ebenfalls in E liegt.

(Quelle Abitur BW 2012 Aufgabe 8)

Lösung A8/12

Aufgabe A6/13

Die Gerade g verläuft durch die Punkte A(1|-1|3) und B(2|-3|0).
Die Ebene E wird von g orthogonal geschnitten und enthält den Punkt C(4|3|-8).
Bestimmen Sie den Schnittpunkt S von g und E.
Untersuchen Sie, ob S zwischen A und B liegt.

(Quelle Abitur BW 2013 Aufgabe 6)

Lösung A6/13

Aufgabe A7/13

Gegeben sind die beiden Ebenen
	E₁: 2x₁-2x₂+x₃ =-1 und $Fit in Mathe Latex: 03a273d5a0eab641b23b76ba50366ef0.png$
Zeigen Sie, dass die beiden Ebenen parallel zueinander sind. Die Ebene E₃ ist parallel E₁ und E₂ und hat von beiden Ebenen denselben Abstand. Bestimmen Sie eine Gleichung der Ebene E₃.

(Quelle Abitur BW 2013 Aufgabe 7)

Lösung A7/13

Aufgabe A6/14

Gegeben sind die Ebenen E: x₁+x₂=4 und F: x₁+x₂+2x₃=4.
a)	Stellen Sie die Ebenen E und F in einem gemeinsamen Koordinatensystem dar. Geben Sie eine Gleichung der Schnittgeraden von E und F an.
b)	Die Ebene G ist parallel zur x₁-Achse und schneidet die x₁x₂-Ebene in derselben Spurgeraden wie die Ebene F. Geben Sie eine Gleichung der Ebene G an.

(Quelle Abitur BW 2014 Aufgabe 6)

Lösung A6/14

Aufgabe A7/14

Gegeben sind die die Punkte A(1|10|1), B(-3|13|1) und C(2|3|1).
Die Gerade g verläuft durch A und B.
Bestimmen Sie den Abstand des Punktes C von der Geraden g.

(Quelle Abitur BW 2014 Aufgabe 7)

Lösung A7/14

Lösung 7/14 umständlich

Aufgabe A9/14

Gegeben sind der Mittelpunkt einer Kugel sowie eine Ebene.
Die Kugel berührt diese Ebene.
Beschreiben Sie, wie man den Kugelradius und den Berührpunkt bestimmen kann.

(Quelle Abitur BW 2014 Aufgabe 9)

Lösung A9/14

Aufgabe A6/15

Gegeben sind die drei Punkte A(4\|0\|4), B(0\|4\|4) und C(6\|6\|2).
a)	Zeigen Sie, dass das Dreieck ABC gleichschenklig ist.
b)	Bestimmen Sie die Koordinaten eines Punktes, der das Dreieck zu einem Parallelogramm ergänzt. Veranschaulichen Sie durch eine Skizze, wie viele solche Punkte es gibt.

(Quelle Abitur BW 2015 Aufgabe 6)

Lösung A6/15

Aufgabe A7/15

Gegeben ist die Ebene E: 4x₁+3x₃=12.
a)	Stellen Sie E in einem Koordinatensystem dar.
b)	Bestimmen Sie alle Punkte der x₃-Achse, die von E den Abstand 3 haben.

(Quelle Abitur BW 2015 Aufgabe 7)

Lösung A7/15

Aufgabe A6/16

Gegeben ist die Gerade 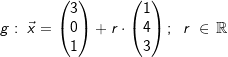$Fit in Mathe Latex: 85e1885214b6e5d48d9e1be3e52f93b4.png$ .
a)	Untersuchen Sie, ob es einen Punkt auf g gibt, dessen drei Koordinaten identisch sind.
b)	Die Gerade h verläuft durch Q(8\|5\|10) und schneidet g orthogonal. Bestimmen Sie eine Gleichung von h.

(Quelle Abitur BW 2016 Aufgabe 6)

Lösung A6/16

Aufgabe A7/16

Gegeben ist die Ebene E: 4x₁+4x₂+7x₃=28.
Es gibt zwei zu E parallele Ebenen F und G, die vom Ursprung den Abstand 2 haben. Bestimmen Sie jeweils eine Gleichung von F und G.

(Quelle Abitur BW 2016 Aufgabe 7)

Lösung A7/16

Aufgabe A9/16

Von zwei Kugeln K₁ und K₂ sind die Mittelpunkte M₁ und M₂ sowie die Radien r₁ und r₂ bekannt. Die Kugeln berühren einander von außen im Punkt B.
Beschreiben Sie ein Verfahren, mit dem man B bestimmen kann.

(Quelle Abitur BW 2016 Aufgabe 9)

Lösung A9/16

Aufgabe A5/17

Gegeben sind die Ebene E: x₁+3x₂=6 und 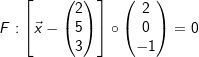$Fit in Mathe Latex: 9cf82f4f7e566d6ac23fba27f3f7822c.png$ .
a)	Stellen Sie die Ebene E in einem Koordinatensystem dar.
b)	Bestimmen Sie eine Gleichung der Schnittgeraden von E und F.
c)	Ermitteln Sie eine Gleichung einer Geraden, die in E enthalten ist und mit F keinen Punkt gemeinsam hat.

(Quelle Abitur BW 2017 Aufgabe 5)

Lösung A5/17

Aufgabe A6/17

Gegeben sind eine Ebenen E, ein Punkt P in E sowie ein weiterer Punkt S, der nicht in E liegt.
Der Punkt S ist die Spitze eines geraden Kegels, dessen Grundkreis in E liegt und durch P verläuft. Die Strecke $Fit in Mathe Latex: a97a9338e0d87010226df5b47ba0f9cd.png$ bildet den Durchmesser des Grundkreises.
Beschreiben Sie ein Verfahren, mit dem man die Koordinaten des Punktes Q bestimmen kann.

(Quelle Abitur BW 2017 Aufgabe 6)

Lösung A6/17

Aufgabe A5/18

Gegeben sind die Ebenen E: 2x₁+2x₂+x₃=5 und die Gerade 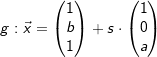$Fit in Mathe Latex: b03b17956fb96e41892e9e2527a50b24.png$ .
a)	Bestimmen Sie die Werte für a und b.
b)	Geben Sie eine Gleichung h einer Geraden an, die ebenfalls in E liegt und senkrecht zur Geraden g verläuft.

(Quelle Abitur BW 2018 Aufgabe 5)

Lösung A5/18

Aufgabe A6/18

Gegeben ist die Ebene E: x₁+2x₂-x₃=4.
a)	Begründen Sie, dass die Spurpunkte von E die Ecken eines gleichschenkligen Dreiecks bilden.
b)	Die Ebene 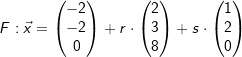$Fit in Mathe Latex: d3256adec8f94e2a7ff0d42ede512d8b.png$ schneidet die Ebene E. Bestimmen Sie die Gleichung der Schnittgeraden s von E und F.

(Quelle Abitur BW 2018 Aufgabe 6)

Lösung A6/18

Du befindest dich hier:

Abituraufgaben allg. Gymnasium Pflichtteil Analytische Geometrie III