 |
2008 Abituraufgaben allg. Gymnasium Pflichtteil |
Aufgaben des Prüfungsjahres 2008 BW |
Aufgabe A2
| G ist eine Stammfunktion der Funktion g mit g(x)=2-3 ⋅ sin(4x). Der Punkt P(0|1) liegt auf dem Schaubild von G. Bestimmen Sie einen Funktionsterm von G. |
| |
Lösung A2
Aufgabe A4
| Für eine ganzrationale Funktion h zweiten Grades gilt: T(-1|-4) ist der Tiefpunkt und Q(2|5) ein weiterer Punkt ihres Schaubilds. Ermitteln Sie eine Funktionsgleichung von h. |
| |
Lösung A4
Aufgabe A5
Gegeben sind die Schaubilder von vier Funktionen, jeweils mit sämtlichen Asymptoten.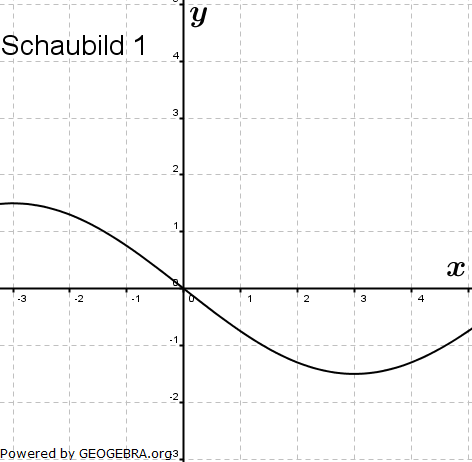 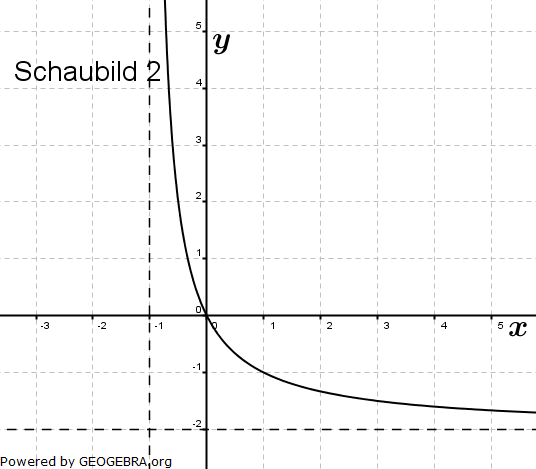 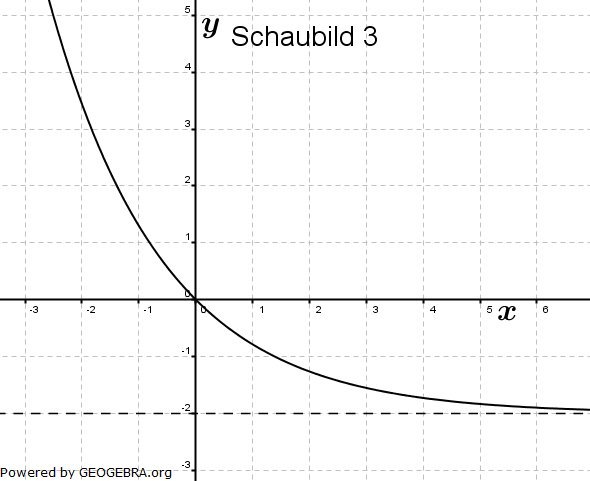 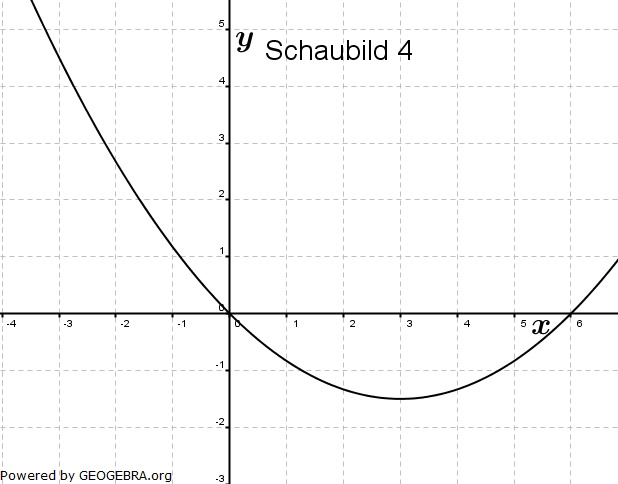 Drei dieser Schaubilder werden beschrieben durch die Funktionen f, g und h mit 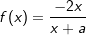 , g(x)=-2+b∙e-0,5x, h(x)=c∙x2-x , g(x)=-2+b∙e-0,5x, h(x)=c∙x2-x |
|
| a) | Ordnen Sie den Funktionen f, g und h das jeweils passende Schaubild zu. Begründen Sie Ihre Zuordnung. |
| b) | Bestimmen Sie die Werte für a, b und c. |
| |
Lösung A5
Aufgabe A6
Die Ebene E geht durch die Punkte A(1,5|0|0), B(0|3|0) und C(0|0|6). Untersuchen Sie, ob die Gerade 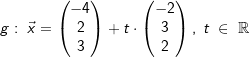 parallel zur Ebene E verläuft. parallel zur Ebene E verläuft. |
| |
Lösung A6
Aufgabe A7
Die Ebene E geht durch die Punkte A(1,5|0|0), B(0|3|0) und C(0|0|6). Untersuchen Sie, ob die Gerade 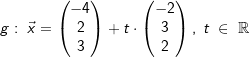 parallel zur Ebene E verläuft. parallel zur Ebene E verläuft. |
| |
Lösung A7
Aufgabe A8
Gegeben sind die beiden Ebenen 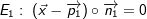 und und 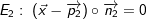 . Beschrieben Sie ein Verfahren, mit dem man anhand dieser Normalengleichungen die gegenseitige Lage der beiden Ebenen untersuchen kann. . Beschrieben Sie ein Verfahren, mit dem man anhand dieser Normalengleichungen die gegenseitige Lage der beiden Ebenen untersuchen kann. |
| |
Lösung A8
| Du befindest dich hier: |
| 2008 Abituraufgaben allg. Gymnasium Pflichtteil |




 .
. .
.

