 |
2006 Abituraufgaben allg. Gymnasium Pflichtteil |
Aufgaben des Prüfungsjahres 2006 BW |
.
.Aufgabe A3
| De Funktion f mit f(x)=x3-3x2-x+3 hat die Nullstelle x1=1. Bestimmen Sie die weiteren Nullstellen. |
 Eine Frage stellen... |
Lösung A3
Aufgabe A4
| Das Schaubild einer ganzrationalen Funktion dritten Grades berührt die x-Achse im Ursprung. Der Punkt H(1|1) ist der Hochpunkt des Schaubilds. Bestimmen Sie die Funktionsgleichung. |
| Eine Frage stellen... |
Lösung A4
Aufgabe A5
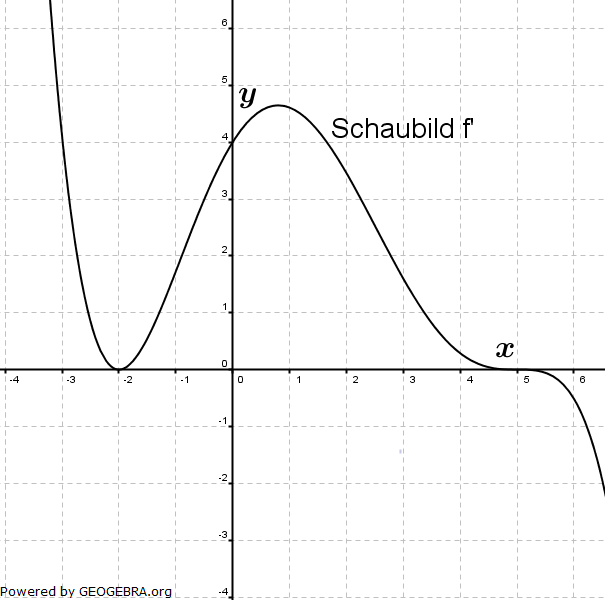
| Die Abbildung zeigt das Schaubild der Ableitungsfunktion f' einer Funktion f. Geben Sie für jeden der folgenden Sätze an, ob er richtig, falsch oder nicht entscheidbar ist. |
 |
|
| (1) | Das Schaubild von f hat bei x=-2 einen Tiefpunkt. | |
| (2) | Das Schaubild von f hat für -3≤x≤6 genau zwei Wendepunkte. | |
| (3) | Das Schaubild von f verläuft im Schnittpunkt mit der y–Achse steiler als die erste Winkelhalbierende. | |
| (4) | f(0)>f(5). | |
| Eine Frage stellen... |
Lösung A5
Aufgabe A6
| Gegeben sind die Ebene | |
| E: -2x1+x2-2x3+15=0 und die Gerade | |
 . |
|
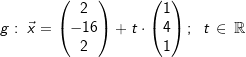| a) | Zeigen Sie, dass E zu g parallel ist. |
| b) | Bestimmen Sie den Abstand der Geraden g von der Ebene E. |
| Eine Frage stellen... |
Lösung A6
Aufgabe A7
| Gegeben sind die Ebenen E1 und E2 mit | |
| E1: 4x1+3x2+2x3=12 | |
| E2: 3x1+2x2=6 | |
| Stellen Sie die beiden Ebenen in einem Koordinatensystem dar. Zeichnen Sie die Schnittgerade der beiden Ebenen ohne weitere Rechnung ein. | |
| Eine Frage stellen... |
Lösung A7
Aufgabe A8
| Gegeben sind zwei Punkte A und B. Diese liegen bezüglich einer Ebene E symmetrisch. | |
| Beschreiben Sie ein Verfahren zur Bestimmung einer Gleichung von E. |
| Eine Frage stellen... |
Lösung A8
| Du befindest dich hier: |
| 2006 Abituraufgaben allg. Gymnasium Pflichtteil |
