 |
2005 Abituraufgaben allg. Gymnasium Pflichtteil |
Aufgaben des Prüfungsjahres 2005 BW |
Aufgabe A1
| Bilden Sie die Ableitung der Funktion f mit f(x)=x3⋅ e2x. |
| |
Lösung A1
Aufgabe A4
Gegeben ist die Funktion f mit 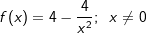 . .Geben Sie die Asymptoten des Schaubilds von f an. Skizzieren Sie damit das Schaubild von f. Ermitteln Sie eine Gleichung der Normalen im Punkt P(2|f(2)). |
| |
Lösung A4
Aufgabe A5
Gegeben sind die Schaubilder der Funktion f mit f(x)=x2ex, ihrer Ableitungsfunktion f', einer Stammfunktion F von f und der Funktion g mit 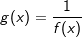 . . |
||||
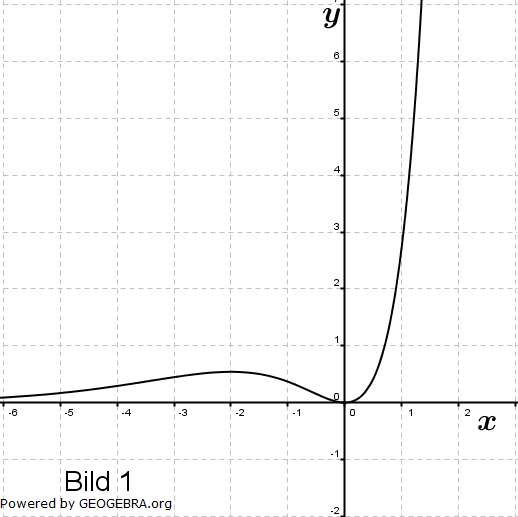 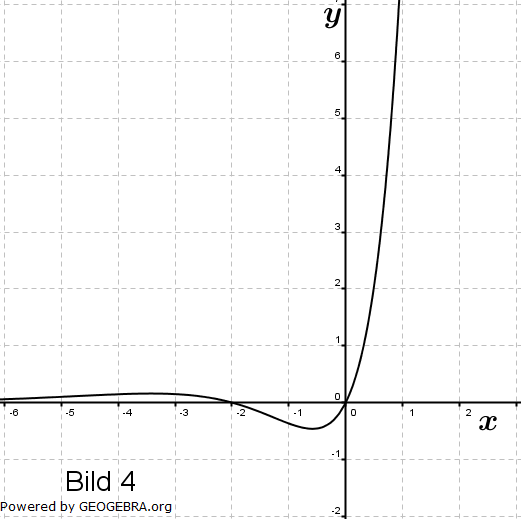 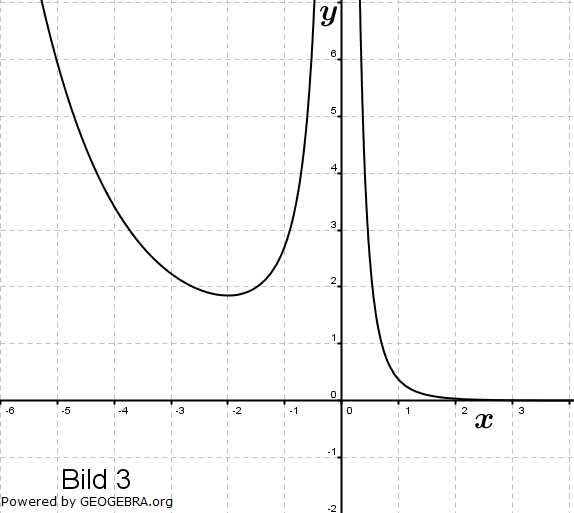 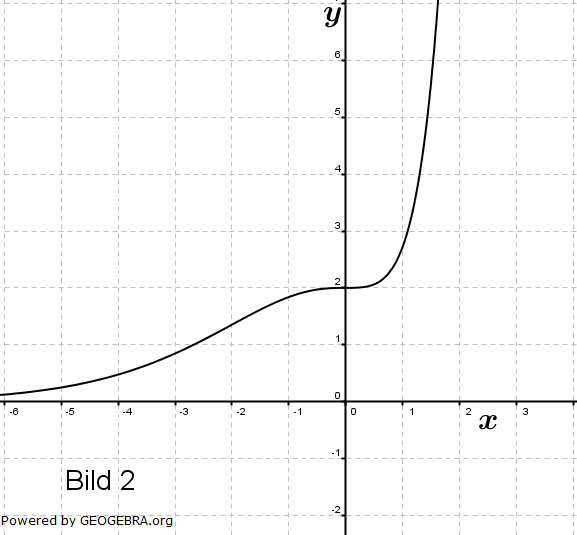 |
||||
|
| |
Lösung A5
Aufgabe A6
| Lösen Sie das lineare Gleichungssystem | |
| x1+4x2+x3=10 | |
| x1+2x2+x3=8 | |
| x1+ x2-x3=3 | |
| Wie lässt sich ein solches Gleichungssystem und seine eindeutige Lösung geometrisch deuten? | |
| |
Lösung A6
Aufgabe A7
Ermitteln Sie eine Koordinatengleichung der Ebene, die den Punkt A(2|-1|-2) und die Gerade 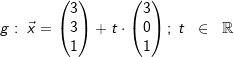 enthält. enthält. |
| |
Lösung A7
Aufgabe A8
| Gegeben sind die Ebene E und ein Punkt P, der nicht auf E liegt. P wird an E gespiegelt. Beschreiben Sie ein Verfahren, um den Bildpunkt P' zu bestimmen. Fertigen Sie eine Skizze an. |
| |
Lösung A8
| Du befindest dich hier: |
| 2005 Abituraufgaben allg. Gymnasium Pflichtteil |




 .
.

