 |
2004 Abituraufgaben allg. Gymnasium Pflichtteil |
Aufgaben des Prüfungsjahres 2004 BW |
Aufgabe A1
Bilden Sie die Ableitung der Funktion f mit 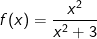 und vereinfachen Sie f'(x). und vereinfachen Sie f'(x). |
| |
Lösung A1
Aufgabe A4
Gegeben ist die Funktion 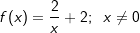 . .Das Schaubild von f hat im Punkt P(1|v) die Tangente t. Ermitteln Sie eine Gleichung von t. Die Tangente t schneidet die x–Achse im Punkt S. Bestimmen Sie die Koordinaten von S. |
| |
Lösung A4
Aufgabe A5
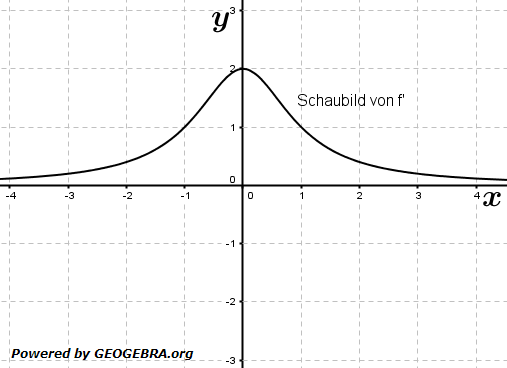
| Die Abbildung zeigt das Schaubild der Ableitungsfunktion f' einer Funktion f Welche der folgenden Aussagen über die Funktion f sind wahr, falsch oder unentscheidbar? |
 |
|
| (1) | f ist streng monoton wachsend für -3<x<3. | |
| (2) | Das Schaubild von f hat mindestens einen Wendepunkt. | |
| (3) | Das Schaubild von f ist symmetrisch zur y–Achse. | |
| (4) | Es gilt f(x)>0 für alle x ∈ [-3;3]. | |
| |
Lösung A5
Aufgabe A6
| Gegeben sind die Gerade g und die Ebene E durch | |
 |
|
| E: 4x1-2x2+4x3=11. | |
| Prüfen Sie nach, ob der Punkt A(3|0|2) auf der Geraden g liegt. Zeigen Sie: Die Gerade g ist orthogonal zur Ebene E. Bestimmen Sie die Koordinaten desjenigen Punktes der Ebene E, welcher vom Punkt A den kleinsten Abstand hat. |
|
| |
Lösung A6
Aufgabe A7
Ermitteln Sie eine Koordinatengleichung der dargestellten Ebene. |
| |
Lösung A7
Aufgabe A8
| Gegeben sind im Raum eine Gerade g und ein Punkt A, der nicht auf g liegt. Beschreiben Sie ein Verfahren zur Bestimmung des Abstandes von A zu g. |
| |
Lösung A8
| Du befindest dich hier: |
| 2004 Abituraufgaben allg. Gymnasium Pflichtteil |




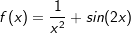 an.
an.

