|
|
Abituraufgaben Leistungskurs Wahlteil Analytische Geometrie
|
|
Aufgaben des Prüfungsjahres 2021 BW |
|
| Dokument mit 2 Aufgaben |
Wahlteil 2021 - Aufgabe B1
Aufgabe B1
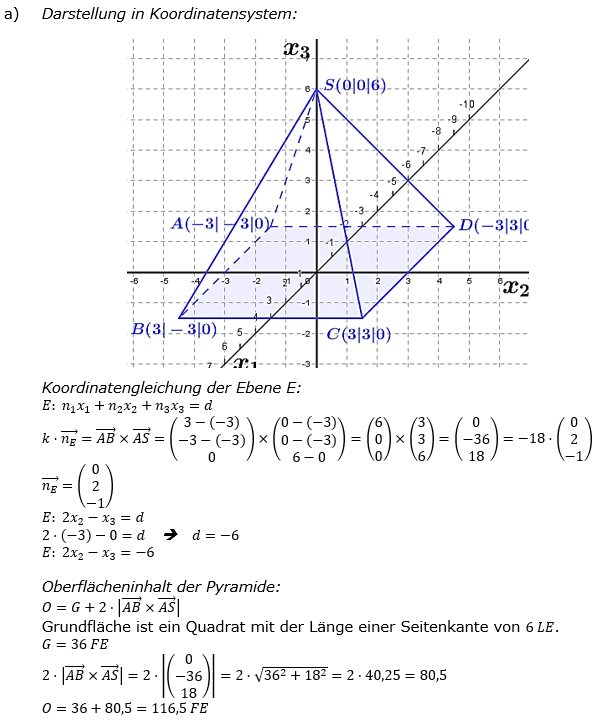
| Gegeben ist eine gerade Pyramide mit quadratischer Grundfläche. Die Eckpunkte der Grundfläche sind A(-3|-3|0), B(3|-3|0), C(3|3|0) und D, die Spitze ist S(0|0|6). Die Ebene E enthält die Punkte A, B und S. |
||
| a) | Stellen Sie die Pyramide in einem geeigneten Koordinatensystem dar. Bestimmen Sie eine Koordinatengleichung der Ebene E. Berechnen Sie den Oberflächeninhalt der Pyramide. (Teilergebnis: E: 2x2-x3=-6) |
|
| b) | Innerhalb der Pyramide gibt es einen Punkt, dessen Abstand von der Grundfläche der Pyramide √5-mal so groß ist wie sein Abstand zu den Seitenflächen. Berechnen Sie die Koordinaten dieses Punktes. |
|
| c) | Betrachtet wird für jedes a > 0 die gerade Pyramide mit folgenden Eigenschaften: | |
| • | A(-a|-a|0), B(a|-a|0), C(a|a|0) und D sind die Eckpunkte der quadratischen Grundfläche. | |
| • | Die x3-Koordinate der Spitze S ist positiv. | |
| • | Die Höhe der Pyramide stimmt mit der Kantenlänge der Grundfläche überein. | |
| M1 ist die Kantenmitte von AB, M2 die Kantenmitte von DS. Zeigen Sie: Die Strecke M1M2 ist orthogonal zur Kante DS. |
||
| |
Lösungslogik B1
 |
Klausuraufschrieb B1 a)
Klausuraufschrieb B1 b-c)
Wahlteil 2021 - Aufgabe B2
Aufgabe B2
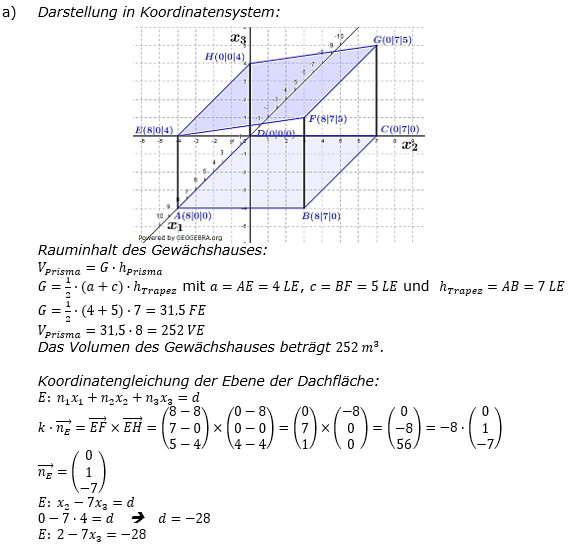
| Eine Firma stellt Gewächshäuser her. Die Ecken der Grundfläche dieser Gewächshäuser können modellhaft durch die Punkte A(8|0|0), B(8|7|0), C(0|7|0) und D(0|0|0) beschrieben werden. In diesen Ecken stehen senkrecht zur Grundfläche Pfosten, die das Dach des Gewächshauses tragen (alle Koordinatenangaben in Meter). |
|
| a) | Bei einem dieser Gewächshäuser können die Ecken der Dachfläche durch die Punkte E(8|0|4), F(8|7|5), G(0|7|5) und H(0|0|4) beschrieben werden. Stellen Sie dieses Gewächshaus in einem geeigneten Koordinatensystem dar. Berechnen Sie den Rauminhalt dieses Gewächshauses. Ermitteln Sie eine Koordinatengleichung der Ebene, die die Lage der Dachfläche beschreibt. |
| b) | Die Firma bietet die Gewächshäuser mit unterschiedlichen Neigungen der Dachfläche an. Die Lage jeder dieser Dachflächen kann durch eine Ebene beschrieben werden, die zur Schar Ea: ax2-7x3=7a-35 mit a > 0 gehört. Berechnen Sie den Wert von a, für den die Neigung der Dachfläche 30 ° beträgt. Es gibt eine Gerade g, die in allen Ebenen der Ebenenschar liegt. Bestimmen Sie eine Gleichung dieser Geraden g. Untersuchen Sie, für welche Werte von a im gesamten Gewächshaus eine Mindesthöhe von 2 m gegeben ist. |
| |
Lösungslogik B2
 |
Klausuraufschrieb B2 a)
Klausuraufschrieb B2 b)
| Du befindest dich hier: |
| Abituraufgaben Leistungskurs Wahlteil Analytische Geometrie |