|
|
Abituraufgaben Leistungskurs Wahlteil Analytische Geometrie 2022
|
|
Aufgaben des Prüfungsjahres 2022 BW |
|
| Dokument mit 2 Aufgaben |
Wahlteil 2022 - Aufgabe B1
Aufgabe B1
| Für k ∈ R mit 0 < k ≤ 6 werden die Pyramiden ABCD mit A(0|0|0), B(4|0|0), C(0|4|0) und Dk (0|0|k) betrachtet (siehe Abbildung), |
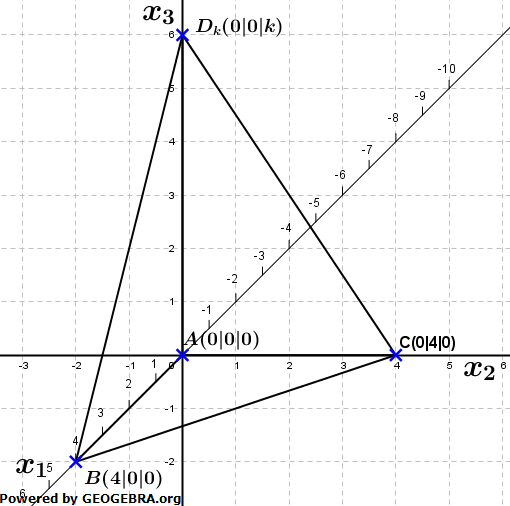 |
|
| a) | Begründen Sie, dass das Dreieck BCDk gleichschenklig ist. Der Mittelpunkt der Strecke BC ist M(2|2|0). 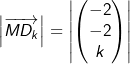 ist die Länge einer Höhe des Dreiecks BCDk. ist die Länge einer Höhe des Dreiecks BCDk.Bestimmen Sie den Flächeninhalt des Dreiecks BCDk. |
|
Für jeden Wert von k liegt die Seitenfläche BCDk in der Ebene 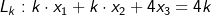 . . |
||
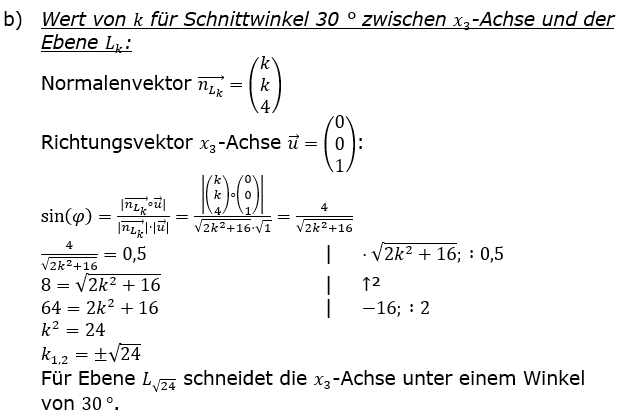
| b) | Ermitteln Sie denjenigen Wert von k, für den die Größe des Winkels, unter dem die x3-Achse die Ebene Lk schneidet, 30 ° beträgt. | |
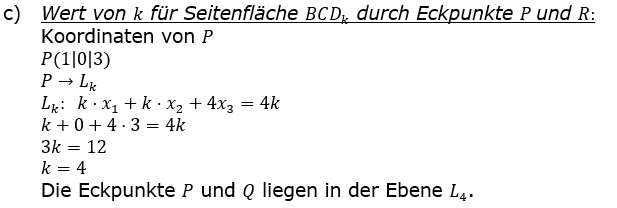
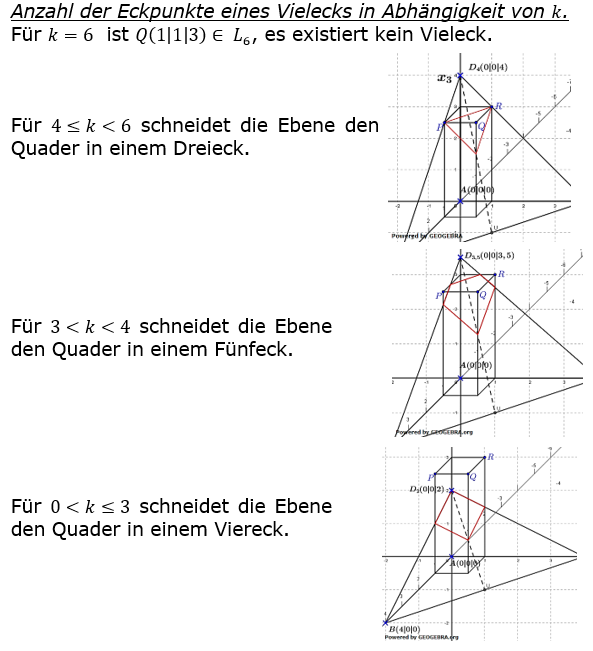
| c) | 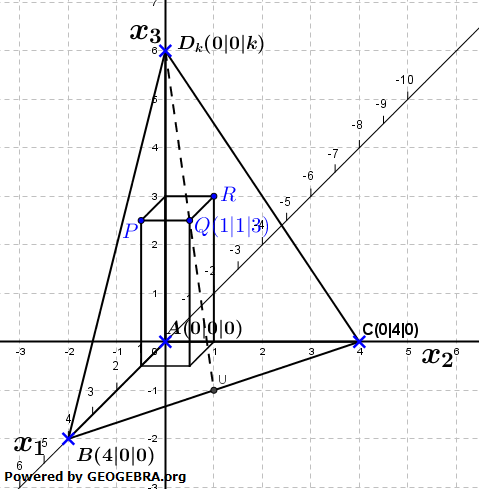 Zusätzlich zu den Pyramiden wird der in nebenstehender Abbildung gezeigte Quader betrachtet. Die Punkte A und Q(1|1|3) sind Eckpunkte des Quaders, die Seitenfläche des Quaders sind parallel zu den Koordinatenebenen. Zusätzlich zu den Pyramiden wird der in nebenstehender Abbildung gezeigte Quader betrachtet. Die Punkte A und Q(1|1|3) sind Eckpunkte des Quaders, die Seitenfläche des Quaders sind parallel zu den Koordinatenebenen.Für k=6 enthält die Seitenfläche BCDk der Pyramide den Eckpunkt Q des Quaders. Für kleinere Werte von k schneidet die Seitenfläche BCDk den Quader in einem Vieleck. Für einen Wert von k verläuft die Seitenfläche BCDk durch die Eckpunkte P und R des Quaders. Bestimmen Sie diesen Wert von k. Geben Sie in Abhängigkeit von k die Anzahl der Eckpunkte des Vielecks an, in dem die Seitenfläche BCDk den Quader schneidet. |
|
| d) | 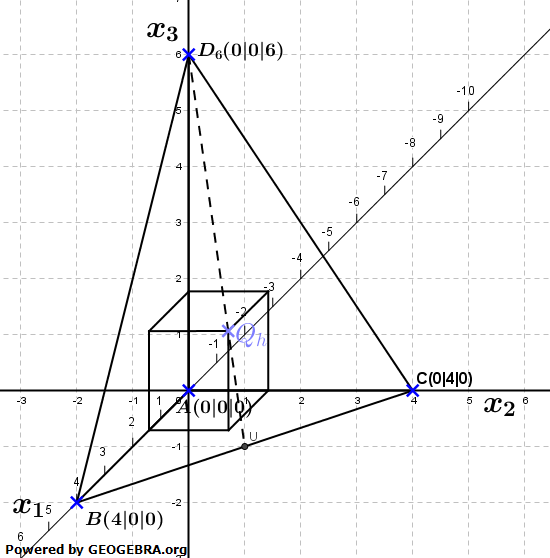 Nun wird die Pyramide ABCD6 , d.h. diejenige für k=6, betrachtet. Nun wird die Pyramide ABCD6 , d.h. diejenige für k=6, betrachtet.Dieser Pyramide werden Quader einbeschrieben (vgl. Abbildung). Die Grundflächen der Quader liegen in der x1 x2-Ebene, haben den Eckpunkt A gemeinsam und sind quadratisch. Die Höhe h der Quader durchläuft alle reellen Werte mit 0 < h < 6. Für jeden Wert von h liegt der Eckpunkt Qh in der Seitenfläche BCD6 der Pyramide. Ermitteln Sie die Koordinaten des Punktes Qh. |
|
| |
Lösungslogik B1
Klausuraufschrieb B1 a)-b)
Klausuraufschrieb B1 c)
Klausuraufschrieb B1 d)
Wahlteil 2022 - Aufgabe B2
Aufgabe B2
Gegeben sind die Geradenschar 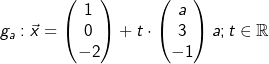 . und die Gerade . und die Gerade 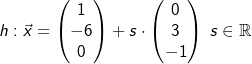 . . |
|
| a) | Beschreiben Sie die besondere Lage der Gerade h im Koordinatensystem. Zeigen Sie, dass die Gerade h zur Schar ga gehört. Alle Geraden der Schar ga liegen in einer Ebene E. Bestimmen Sie eine Koordinatengleichung der Ebene E. (Teilergebnis: E: x2+3x3=-6) |
| b) | Bestimmen Sie denjenigen Wert von a, für den ga die x2-Achse schneidet. Es gibt zwei Geraden der Schar ga , die die Gerade h im Winkel 45 ° schneiden. Ermitteln Sie die zugehörigen Werte von a. |
| c) | Bestimmen Sie eine Gleichung einer Gerade, die von allen Geraden der Schar ga den Abstand 40 besitzt und zu allen Geraden der Schar ga windschief verläuft. |
| |
Lösungslogik B2
Klausuraufschrieb B2 a)
Klausuraufschrieb B2 b)-c)
| Du befindest dich hier: |
| Abituraufgaben Leistungskurs Wahlteil Analytische Geometrie 2022 |