Abitur allg. Gymnasium Leistungskurs Wahlteil Analysis 2021 BW

Wahlteil 2021 - Aufgabe 1.1

Aufgabe A1.1

Das Gelände eines Abenteuerspielplatzes besteht aus einer Hochfläche, an die sich ein Hang mit einer Senke anschließt. Die Profillinie des Geländes wird für -3 ≤ x ≤ 0 durch die Gerade mit der Gleichung y=5 und für 0 ≤ x ≤ 11 durch den Graphen der Funktion f mit f(x)=0,0008x⁴-0,12x²+5 beschrieben.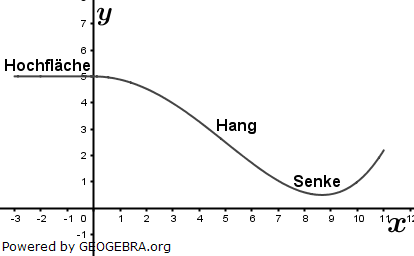
Die Abbildung zeigt diese Profillinie. (1 LE entspricht 1 m)

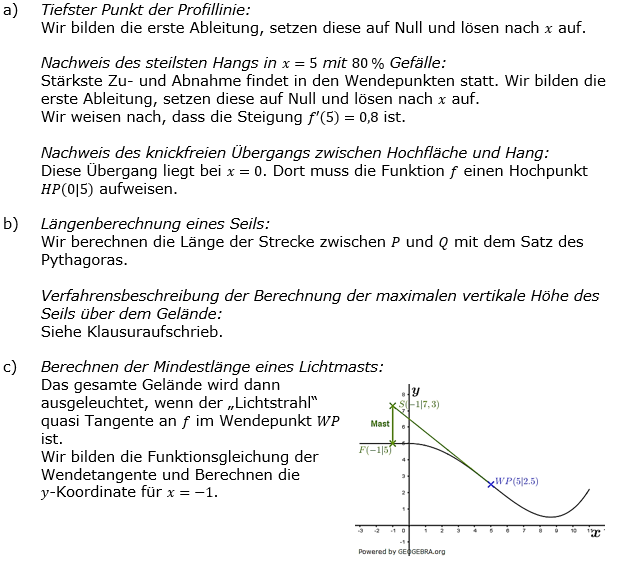
a)	Berechnen Sie die Koordinaten des tiefsten Punktes der Profillinie. Weisen Sie rechnerisch nach, dass der Hang zwischen Hochfläche und Senke an der Stelle x=5 am steilsten abfällt und dort ein Gefälle von 80 % hat. Zeigen Sie, dass die Profillinie beim Übergang von der Hochfläche zum Hang knickfrei ist. (Teilergebnis: Der tiefste Punkt hat die y-Koordinate 0,5)
b)	Zwischen zwei Befestigungspunkten, die im Modell durch P(5\|f(5)) und Q(10\|f(10)) dargestellt werden, wird ein Seil straff gespannt. Berechnen Sie die Länge des Seils. Beschreiben Sie ein Verfahren, mit dem man die maximale vertikale Höhe des Seils über dem Gelände berechnen kann.
c)	Auf der Hochfläche, einen Meter vom Übergang zum Hang entfernt, steht ein vertikaler Lichtmast, von dem aus das gesamte Gelände ausgeleuchtet werden kann. Berechnen Sie die Mindestlänge dieses Lichtmasts.
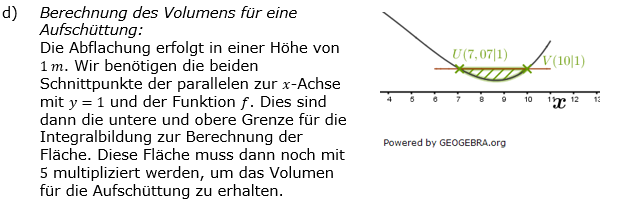
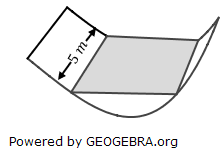
d)	Bei einem Umbau soll die Senke auf 5 m Länge so mit Sand aufgefüllt werden, dass eine horizontale rechteckige Fläche entsteht, die 0,5 m oberhalb des tiefsten Punktes der Senke liegt. Berechnen Sie das Volumen des dafür benötigten Sandes.

Lösungslogik A1.1

Klausuraufschrieb A1.1 a-b)

Klausuraufschrieb A1.1 c-d)

Wahlteil 2021 - Aufgabe 1.2

Aufgabe A1.2

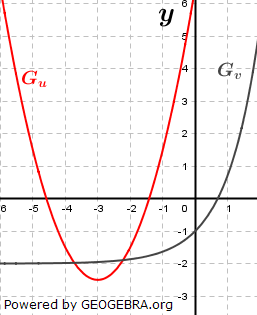
Abgebildet sind die Graphen G_u und G_v zweier Funktionen u und v.
Die Funktion f ist gegeben durch f(x)=v(u(x)). Bestimmen Sie f(-1).
Ermitteln Sie die Anzahl der Nullstellen von f im abgebildeten Bereich.

Das Gelände eines Abenteuerspielplatzes besteht aus einer Hochfläche, an die sich ein Hang mit einer Senke anschließt. (Abitur allg. bildendes Gymnasium Wahlteilaufgaben Leistungsfach Analysis 2021-12 / © by www.fit-in-mathe-online.de)

Lösungslogik A1.2

Klausuraufschrieb A1.2

Wahlteil 2021 - Aufgabe 1.3

Aufgabe A1.3

Die Funktion w ist auf 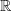$Fit in Mathe Latex: a5b7a189c728560bdaf3713d33b15508.png$ definiert und zweimal differenzierbar.
Für die Funktion g gilt g(x)=e^w(x)-2.
Zeigen Sie: Wenn x=0 eine Wendestelle von w und von g ist, dann hat der Graph von w bei x=0 eine waagrechte Tangente.

Klausuraufschrieb A1.3

Wahlteil 2021 - Aufgabe 2.1

Aufgabe A2.1

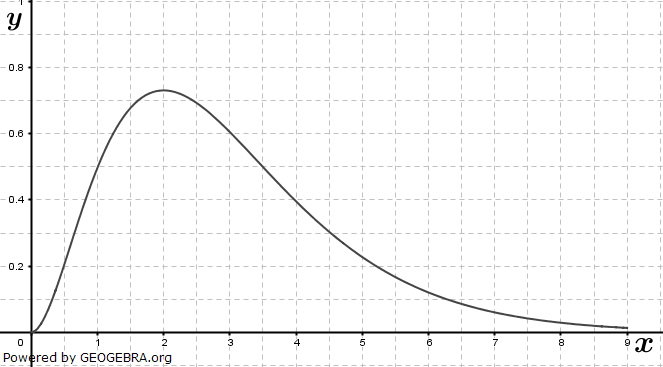
Die Funktion f beschreibt für 0 ≤ t ≤ 8 modellhaft die Wachstumsgeschwindigkeit eines Apfelbaums, der zu Beobachtungsbeginn 0,8 m hoch ist (t in Jahren nach Beobachtungsbeginn, f(t) in Meter pro Jahr).
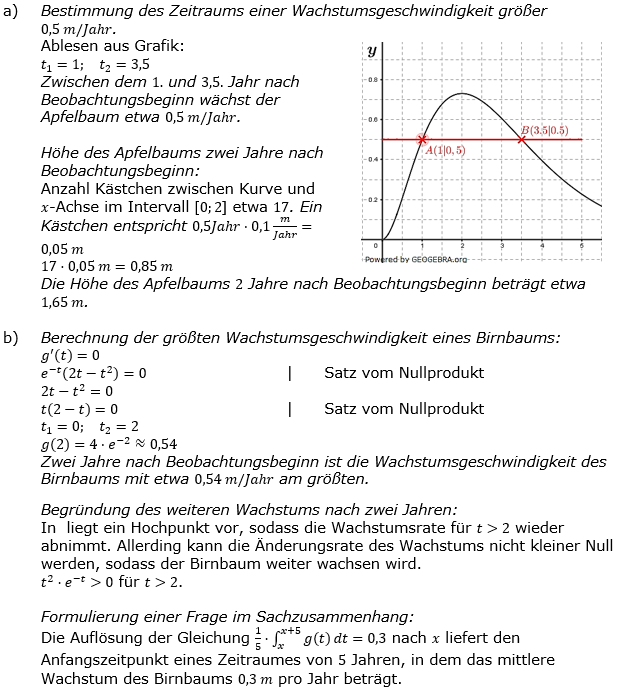
a)	Die Abbildung in der Anlage zeigt den Graphen G_f von f. Bestimmen Sie die Länge des Zeitraums, in dem die Wachstumsgeschwindigkeit des Apfelbaums größer als 0,5 Meter pro Jahr ist. Bestimmen Sie die Höhe des Apfelbaums zwei Jahre nach Beobachtungsbeginn.
Die Wachstumsgeschwindigkeit eines Birnbaums, der zu Beobachtungsbeginn 1,2 m hoch ist, wird für 0 ≤ t ≤ 8 modellhaft beschrieben durch die Funktion g mit g(t)=t²⋅e^-t (t in Jahren nach Beobachtungsbeginn, g(t) in Meter pro Jahr). Für die Ableitungen der Funktion g gilt: g'(t)=2t∙e^-t-t²e^-t; g''(t)=2e^-t-4t⋅e^-t+t²∙e^-t.
b)	Berechnen Sie den Zeitpunkt, zu dem die Wachstumsgeschwindigkeit des Birnbaums am größten ist, und geben Sie diese Wachstumsgeschwindigkeit an. Begründen Sie, dass der Birnbaum ab diesem Zeitpunkt weiterhin wächst, die Wachstumsgeschwindigkeit jedoch ständig abnimmt. Formulieren Sie eine Frage im Sachzusammenhang, die auf die Gleichung 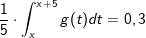$Fit in Mathe Latex: 664093092342e8013e38d9d8a74f1e07.png$ führt.
c)	Zeigen Sie, dass für 0 ≤ t ≤ 8 die Funktion h mit h(t)=(-t²-2t-2)⋅e^-t+3,2 die Höhe des Birnbaums beschreibt (t in Jahren nach Beobachtungsbeginn, h(t) in Meter).
d)	Durch die Zugabe eines Düngers wird das Wachstums von Birnbäumen beeinflusst. Die Höhe eines gedüngten Birnbaums wird durch die Funktion k beschrieben mit k(t)=-2,3e^-t+3,5 ( t ≥ 0 in Jahren nach Beobachtungsbeginn, k(t) in Meter). Die Höhe eines ungedüngten Birnbaums wird weiterhin durch die Funktion h beschrieben. Beide Birnbäume haben zu Beobachtungsbeginn dieselbe Höhe. Berechnen Sie den Zeitpunkt, bis zu dem die Wachstumsgeschwindigkeit des gedüngten Birnbaums größer ist als die des ungedüngten Birnbaums. Untersuchen Sie rechnerisch, welcher der beiden Bäume zuerst eine Höhe von 3,1 m erreicht.
Grafik Wahlteil Anlaysis 2021/2.1 a)
{snippet snippet-graphik-drucken}

Lösungslogik A2.1

Klausuraufschrieb A2.1 a-b)

Klausuraufschrieb A2.1 c-d)

Wahlteil 2021 - Aufgabe 2.2

Aufgabe A2.2

Für jedes t > 0 ist eine Funktion f_t gegeben durch f_t(x)=-4x³+12tx².
a)	Bestimmen Sie die Nullstellen von f_t. Der Graph von f_t schließt mit der x-Achse eine Fläche mit dem Inhalt A_t ein. Ermitteln Sie denjenigen Wert von t, für den 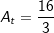$Fit in Mathe Latex: ce198b291ac6224b8f0003dedd5db9fe.png$ gilt.
b)	Für 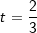$Fit in Mathe Latex: aae5d4c9c36e6519faae51db5b8fb2c5.png$ gibt es Tangenten an den Graphen von f_t, die den Punkt S(3│0) enthalten. Berechnen Sie die x-Koordinaten der zugehörigen Berührpunkte.