 |
|
Abituraufgaben allg. Gymnasium LK 2022 Wahlteil Analysis |
|
Aufgaben des Prüfungsjahres 2022 BW |
|
| Dokument mit 4 Aufgaben |
Wahlteil 2022 - Aufgabe 1.1
Aufgabe A1.1
c)Berechnen Sie die Koordinaten des tiefsten Punktes der Profillinie.
Weisen Sie rechnerisch nach, dass der Hang zwischen Hochfläche und Senke an der Stelle x=5 am steilsten abfällt und dort ein Gefälle von 80 % hat.
Weisen Sie rechnerisch nach, dass der Hang zwischen Hochfläche und Senke an der Stelle x=5 am steilsten abfällt und dort ein Gefälle von 80 % hat.
| Die Abbildung zeigt den Graphen Gf der Funktion f mit f(x)=x3-6x2+8x. |  |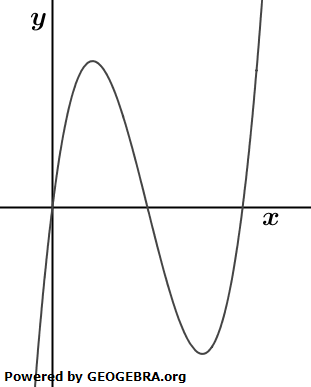
|
| a) | Berechnen Sie die Nullstellen von f. Berechnen Sie die Koordinaten des Wendepunktes W von Gf. Die Gerade t1 ist die Tangente an Gf in W. Zeigen Sie, dass y=-4x+8 eine Gleichung von t1 ist. |
|
| b) | Die Gerade t2 ist die Tangente an Gf im Ursprung O. Die Geraden t1 und t2 schneiden sich im Punkt Q. Berechnen Sie | |
| für das Dreieck OWQ die Weite des Innenwinkels bei Q. Für ein u > 0 ist die Tangente an Gf im Punkt B(u|f(u)) parallel zu t2. Bestimmen Sie den Wert von u. |
||
| c) | Die Funktion I0 mit 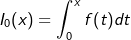 besitzt im Intervall [0;4] ihren maximalen Wert an der Stelle x0. Geben Sie x0 an und begründen Sie Ihre Angabe. |
|
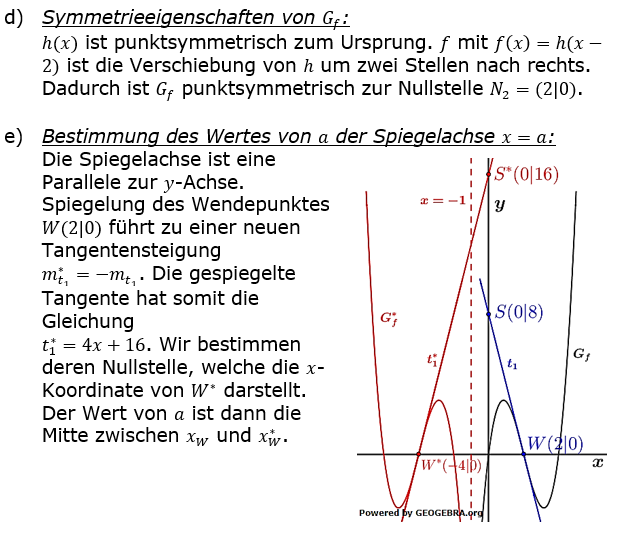
| d) | Für die Funktion h mit h(x)=x3-4x gilt f(x)=h(x-2). Erläutern Sie, welche Symmetrieeigenschaft daraus für Gf folgt. | |
| e) | Der Graph Gf* entsteht durch Spiegelung des Graphen Gf an der Geraden mit der Gleichung x=a. Die Tangente an Gf* im Wendepunkt von Gf* schneidet die y-Achse im Punkt S(0│16). Bestimmen Sie den Wert von a. | |
 Eine Frage stellen... |
Lösungslogik A1.1
Fehler melden...Klausuraufschrieb A1.1 a)
Klausuraufschrieb A1.1 b)-c)
Klausuraufschrieb A1.1 d-e)
Wahlteil 2022 - Aufgabe 1.2
Aufgabe A1.2
Für jedes a>0 ist die Funktion fa gegeben durch 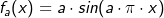 . Die zugehörigen Graphen werden mit Ga bezeichnet. Der Punkt 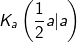 ist ein Hochpunkt von Ga. |
|
| a) | Geben Sie die Periode von fa an. Der Punkt Ha bildet mit den beiden von Ha am wenigsten weit entfernten Tiefpunkten von Ga ein Dreieck. Zeigen Sie, dass der Flächeninhalt dieses Dreiecks unabhängig von a ist. |
| b) | Ermitteln Sie den Wert von a, für den Ha vom Ursprung den Abstand 1 hat |
| c) | Bestimmen Sie eine Gleichung der Kurve K, auf der alle Punkte Ha liegen. Auf K gibt es einen Punkt Ha , in dem die Tangente an K parallel zur Geraden mit der Gleichung y=-2x ist. Bestimmen Sie den Wert von a. |
| Eine Frage stellen... |
Lösungslogik A1.2
Klausuraufschrieb A1.2 a)-b)
Klausuraufschrieb A1.2 c)
Wahlteil 2022 - Aufgabe 2.1
Aufgabe A2.1
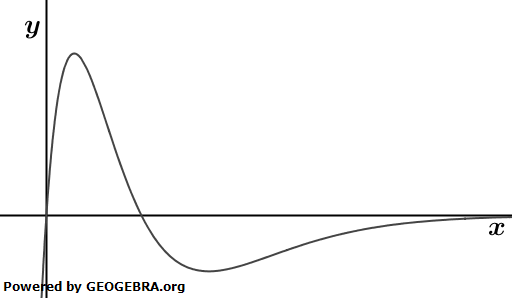
Die Abbildung zeigt den Graphen der Funktion f mit 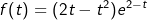 , die für 0≤t≤10 die momentane Änderungsrate des Wasservolumens in einem Becken beschreibt (t in Stunden nach Beobachtungsbeginn, f(t) in Kubikmeter pro Stunde). |
 |
|
| a) | Geben Sie die momentane Änderungsrate des Wasservolumens eine Stunde nach Beobachtungsbeginn an. | |
| Begründen Sie, dass das Wasservolumen in den ersten beiden Stunden nach Beobachtungsbeginn niemals abnimmt. Die momentane Änderungsrate des Wasservolumens besitzt ein Minimum. Bestimmen Sie den Zeitpunkt, zu dem dieses Minimum angenommen wird. (Teilergebnis:  |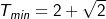
||
| Die Funktion F mit . Ga ist der Graph von ka. | ||
| a) | Geben Sie Gleichungen der Asymptoten des Graphen Ga an. Weisen Sie nach, dass für die Ableitung ka' von ka gilt: 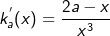 . Zeigen Sie, dass jeder Graph Ga genau einen Extrempunkt besitzt und untersuchen Sie, für welche Werte von a ein Hochpunkt vorliegt. |
|
| b) | Jeder Graph Ga besitzt einen Punkt Pa mit der folgenden Eigenschaft: Die Tangente im Punkt Pa an Ga verläuft durch den Ursprung. Bestimmen sie die x-Koordinate von Pa. |
|
| Eine Frage stellen... |
Lösungslogik A2.1
Klausuraufschrieb A2.2 a)
Klausuraufschrieb A2.2 b)
| Du befindest dich hier: |
| Abituraufgaben allg. Gymnasium LK 2022 Wahlteil Analysis |
