 |
|
Abituraufgaben 2022 Leistungskurs Stochastik
|
|
Aufgaben des Prüfungsjahres 2022 BW |
|
| Dokument mit 2 Aufgaben |
Wahlteil 2022 - Aufgabe C1
Aufgabe C1
| Ein Onlineshop bietet Patronen mit schwarzer Tinte und Patronen mit farbiger Tinte an. | ||
| a) | Erfahrungsgemäß beträgt der Verkaufsanteil der Patronen mit schwarzer Tinte 65 %. Betrachtet wird eine zufällige Auswahl von 100 verkauften Patronen. Es wird davon ausgegangen, dass dabei die Anzahl der Patronen mit schwarzer Tinte binomialverteilt ist. Bestimmen Sie die Wahrscheinlichkeit folgender Ereignisse: |
|
| A: | „Genau 66 der verkauften Patronen sind mit schwarzer Tinte gefüllt.“ | |
| B: | „Die Anzahl der verkauften Patronen mit schwarzer Tinte weicht um mehr als 10 % vom Erwartungswert dieser Anzahl ab.“ | |
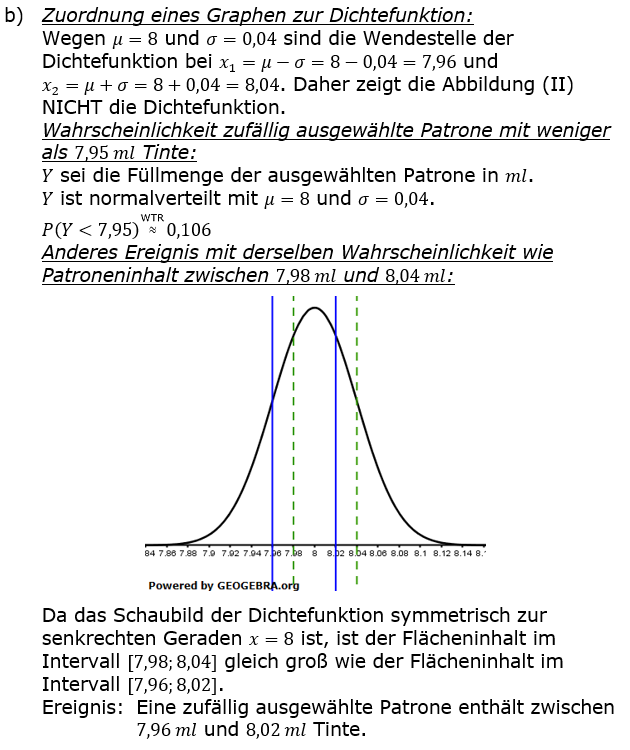
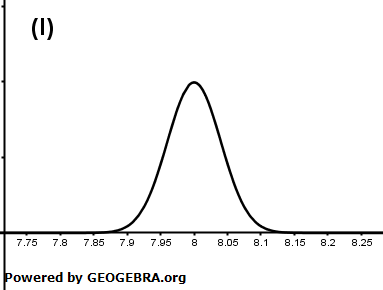
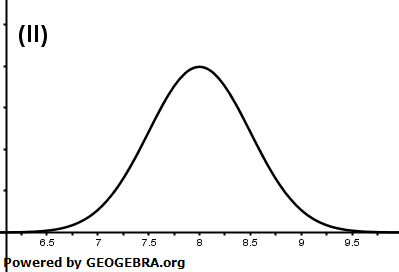
| b) | Im Folgenden werden nur Patronen betrachtet, die mit schwarzer Tinte gefüllt sind. Die Füllmenge einer solchen Patrone wird als normalverteilt mit dem Erwartungswert 8 ml und der Standardabweichung 0,04 ml angenommen. Eine der beiden Abbildungen zeigt den Graphen der zugehörigen Dichtefunktion. |
|
  |
||
| Geben Sie die Abbildung an, die den Graphen der zugehörigen Dichtefunktion nicht zeigt, und begründen Sie Ihre Angabe. Berechnen Sie die Wahrscheinlichkeit dafür, dass eine zufällig ausgewählte Patrone weniger als 7,95 ml Tinte enthält. Betrachtet wird das Ereignis, dass eine zufällig ausgewählte Patrone zwischen 7,98 ml und 8,04 ml Tinte enthält. Geben Sie ein anderes Ereignis im Sachzusammenhang an, welches exakt dieselbe Wahrscheinlichkeit hat. Bestimmen Sie das kleinste Intervall [a;b], so dass die Füllmenge einer zufällig ausgewählten Patrone mit einer Wahrscheinlichkeit von 92 % in [a;b] liegt. |
||
| c) | Betrachtet wird die für x ≥ 0 definierte Funktion f mit 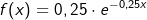 .Weisen Sie nach, dass f eine Dichtefunktion über ihrem Definitionsbereich ist. Die Zeitdauer in Stunden zwischen dem Eingang einer Bestellung im Onlineshop und dem Versand der Ware kann modellhaft durch eine stetige Zufallsgröße mit der Dichtefunktion f beschrieben werden. Mit einer Wahrscheinlichkeit von 85 % wird eine Ware innerhalb von t Stunden nach Eingang der Bestellung versandt. Bestimmen Sie den Wert von t. |
|
 Eine Frage stellen... |
Lösungslogik C1
 |
Klausuraufschrieb C1 a)
Fehler melden...Klausuraufschrieb C1 b)
Klausuraufschrieb C1 c)
Wahlteil 2022 - Aufgabe C2
Aufgabe C2
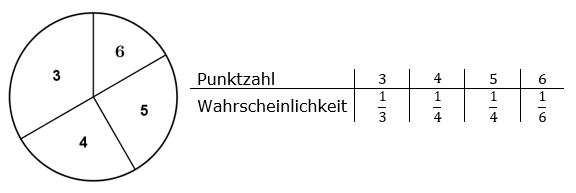
| Beim einmaligen Drehen des abgebildeten Glücksrads erhält man eine von vier möglichen Punktzahlen. Die Tabelle gibt für jede Punktzahl die zugehörige Wahrscheinlichkeit an. | ||
 |
||
| a) | Zehn Personen drehen das Glücksrad jeweils einmal. Bestimmen Sie die Wahrscheinlichkeiten der folgenden Ereignisse: | |
| A: | „Genau zwei Personen erzielen jeweils die Punktzahl 4.“ | |
| B: | „Mindestens drei Personen erzielen jeweils eine Punktzahl, die kleiner als 5 ist.“ | |
| C: | „Die Summe der erzielten Punktzahlen aller zehn Personen ist höchstens 31.“ | |
| b) | Mehrere Spieler verwenden das Glücksrad bei einem Spiel mit folgenden Regeln: | |
| - | Jeder Spieler dreht das Glücksrad einmal. | |
| - | Der Spieler mit der größten erzielten Punktzahl gewinnt. | |
| - | Erzielen mehrere Spieler diese größte Punktzahl, so gewinnt derjenige von ihnen, der als letzter gedreht hat. | |
| Achim ist der erste Spieler und erzielt die Punktzahl 5. Beschreiben Sie, bei welchem weiteren Spielverlauf Achim gewinnt. Die Wahrscheinlichkeit, dass Achim das Spiel gewinnt, ist kleiner als 2 %. Bestimmen Sie die Mindestanzahl der Spieler. |
||
| c) | Ein Spieler vermutet, dass die Wahrscheinlichkeit für die Punktzahl 3 bei dem vorliegenden Glücksrad nicht  ist. Daher soll ein einseitiger Hypothesentest mit einer Stichprobe von 100 Drehungen auf einem Signifikanzniveau von 5 % durchgeführt werden. Dabei soll möglichst vermieden werden, dass irrtümlich von einer zu hohen Wahrscheinlichkeit für die Punktzahl 3 ausgegangen wird.Der Spieler entscheidet sich für die folgende Nullhypothese: „Die Wahrscheinlichkeit für die Punktzahl 3 beträgt höchstens .“Beurteilen Sie, ob dieser Test der genannten Zielsetzung entspricht. Formulieren sie den Fehler zweiter Art im Sachzusammenhang. Beim durchgeführten Test ergibt sich der Ablehnungsbereich A={42;…;100}. Bestimmen Sie die Wahrscheinlichkeit für den Fehler zweiter Art unter der Annahme, dass die Wahrscheinlichkeit für die Punktzahl 3 tatsächlich 40 % beträgt. |
|
| Eine Frage stellen... |
Lösungslogik C2
  |
Klausuraufschrieb C2 a)-b
Klausuraufschrieb C2 c)
| Du befindest dich hier: |
| Abituraufgaben 2022 Leistungskurs Stochastik |
