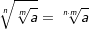|
WIKI zu vermischten Aufgaben mit Wurzeln
|


Einleitung
| Nachdem wir alle Regeln zur Wurzelrechnung nun kennengelernt haben, dient dieses Kapitel dazu, diesbezgl. Aufgaben zu üben und zu wiederholen. Hierzu stellen wir zunächst nochmals die einzelnen Regeln und Merksätze zusammen. |
Basisoperationen
Das detaillierte WIKI findest du unter Basis Rechenoperationen mit Wurzeln.
Teilweises Wurzelziehen
| In bestimmten Fällen ist es möglich, nur von einem Teil des Radikanten die Wurzel zu ziehen. Dies ist immer dann möglich, wenn der Radikant in Faktoren zerlegt werden kann und einer dieser Faktoren ein quadratischer Ausdruck, ein Kubikausdruck bzw. eine Potenz des Wurzelexponenten ist. |
| Aufgaben hierzu findest du unter Teilweises Wurzelziehen. |
Faktor unter die Wurzel bringen
| In manchen Fällen ist es sinnvoll, zur Vereinfachung eines Wurzelterms eine Zahl, die vor einer Wurzel steht, unter die Wurzel zu schreiben. |
| Aufgaben hierzu findest du unter Faktor unter die Wurzel bringen. |
Wurzel Nenner rational machen
Im allgemeinen ist es unüblich bei einem Bruch eine Wurzel im Nenner stehen zu lassen. Mathematikern gefällt der Ausdruck  überhaupt nicht. Sie bemühen sich, die Wurzel im Nenner irgendwie zu beseitigen. überhaupt nicht. Sie bemühen sich, die Wurzel im Nenner irgendwie zu beseitigen.Das lässt sich einfach bewerkstelligen, indem wir den Bruch genau mit der im Nenner stehenden Wurzel erweitern. |
| Aufgaben hierzu findest du unter Wurzel Nenner rational machen. |
Potenzdarstellung von Wurzeln
| In bestimmten Sitationen ist es erforderlich, eine Wurzel in die Potenzschreibweise zu überführen. (z. B. innerhalb der Differenzialrechnug in den Ableitungen). Wurzeln können als Potenz dargestellt werden, indem die Wurzelbasis mit dem Quotienten aus Basisexponent und Wurzelexponent potenziert wird. Werden Wurzeln mit negativem Wurzelexponent oder Basisexponent als Potenz dargestellt, so entspricht die Darstellung dem Kehrwert der positiven Darstellung. |
| Aufgaben hierzu findest du unter Potenzdarstellung von Wurzeln. |
Addition und Subtraktion von Wurzeln
Wann das Addieren möglich ist
| Es können nur Wurzeln mit | |||||||||||||||||||||||||||||
| • | gleichem Radikanten | ||||||||||||||||||||||||||||
| • | gleichem Wurzelexponenten addiert werden. | ||||||||||||||||||||||||||||
Merksatz Addition von Wurzeln
|
|||||||||||||||||||||||||||||
Wann das Subtrahieren möglich ist
| Es können nur Wurzeln mit | |||||||||||||||||||||||||||||
| • | gleichem Radikanten | ||||||||||||||||||||||||||||
| • | gleichem Wurzelexponenten subtrahiert werden. | ||||||||||||||||||||||||||||
Merksatz Subtraktion von Wurzeln
|
|||||||||||||||||||||||||||||
Multiplikation und Division von Wurzeln
Gleichnamige Wurzeln multiplizieren
| Es können Wurzeln mit gleichem Wurzelexponenten multipliziert werden. | |||||||||||||||||||||
Merksatz Multiplikation von gleichnamigen Wurzeln
|
|||||||||||||||||||||
Ungleichnamige Wurzeln multiplizieren
| Wurzeln mit ungleichen Wurzelexponenten müssen vor ihrer Multiplikation durch geeignete Umformung auf den gleichen Wurzelexponenten gebracht werden. | |||||||||||||||||||||
Merksatz Multiplikation von ungleichnamigen Wurzeln
|
|||||||||||||||||||||
Gleichnamige Wurzeln dividieren
| Es können nur Wurzeln mit gleichem Wurzelexponenten dividiert werden. | |||||||||||||||||||||
Merksatz Division von gleichnamigen Wurzeln
|
|||||||||||||||||||||
Ungleichnamige Wurzeln dividieren
| Wurzeln mit ungleichen Wurzelexponenten müssen vor ihrer Division durch geeignete Umformung auf den gleichen Wurzelexponenten gebracht werden. | |||||||||||||||||||||
Merksatz Division von ungleichnamigen Wurzeln
|
|||||||||||||||||||||
Wurzeln potenzieren und radizieren
Wurzeln potenzieren
| Für das Potenzieren von Wurzeln gibt es keine Einschränkung. Jede beliebige Wurzel kann potenziert werden. | |||||||||
Merksatz Potenzieren von Wurzeln
|
|||||||||
Wurzeln radizieren
| Für das Radizieren von Wurzeln gibt es keine Einschränkung. Jede beliebige Wurzel kann radiziert werden. | |||||||||
Merksatz Radizieren von Wurzeln
|
|||||||||
| Hinweis: Beim Radizieren dürfen Wurzelexponenten vertauscht werden. |
|||||||||
| Vermischte Aufgaben mit Wurzeln Aufgabenblatt 1 35 Aufgaben im Blatt |
| Vermischte Aufgaben mit Wurzeln Aufgabenblatt 2 43 Aufgaben im Blatt |
| Vermischte Aufgaben mit Wurzeln Aufgabenblatt 3 52 Aufgaben im Blatt |
| Vermischte Aufgaben mit Wurzeln Aufgabenblatt 4 37 Aufgaben im Blatt |
| Vermischte Aufgaben mit Wurzeln Aufgabenblatt 5 38 Aufgaben im Blatt |
| Vermischte Aufgaben mit Wurzeln Aufgabenblatt 6 24 Aufgaben im Blatt |
| Vermischte Aufgaben mit Wurzeln Aufgabenblatt 7 34 Aufgaben im Blatt |
| Vermischte Aufgaben mit Wurzeln Aufgabenblatt 8 21 Aufgaben im Blatt |
| Vermischte Aufgaben mit Wurzeln Aufgabenblatt 9 34 Aufgaben im Blatt |
| Du befindest dich hier: |
| WIKI zu vermischten Aufgaben mit Wurzeln |

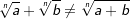
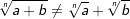
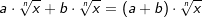
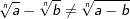
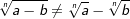
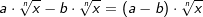

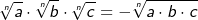
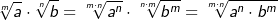
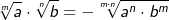
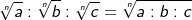
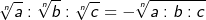
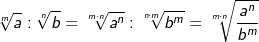
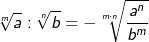
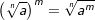
 ) oder zuerst den Radikanden potenziert und dann die Wurzel zieht (
) oder zuerst den Radikanden potenziert und dann die Wurzel zieht ( ).
).