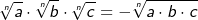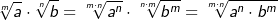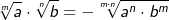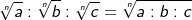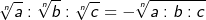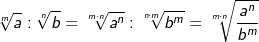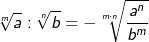|
WIKI zur Multiplikation und Division von Wurzeln |


Einführung
| Dass man Wurzeln nicht so ohne Weiteres addieren bzw. subtrahieren darf, haben wir im Kapitel „Addition und Subtraktion von Wurzeln“ gesehen. Gelten die dort gemachten Einschränkungen aber auch für die Multiplikatioin bzw. Division? Dies sollen dir die folgenden Beispiele zeigen. Beispiele: |
||
Einerseits gilt: |
 |
|
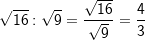 |
||
| Andererseits gilt: | ||
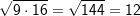 |
||
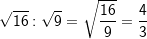 |
||
| Daraus folgt: | ||
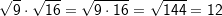 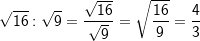 |
||
Multiplikation von Wurzeln
Gleichnamige Wurzeln multiplizieren
| Es können Wurzeln mit gleichem Wurzelexponenten multipliziert werden. Es gibt dabei eine Einschränkung: | |||||||||||||||||||||
| • | Ist der Wurzelexponent gerade, darf die Multiplikation der Wurzelradikanten nicht negativ sein. (a ∙ b ≥ 0). | ||||||||||||||||||||
Merksatz Multiplikation von gleichnamigen Wurzeln
|
|||||||||||||||||||||
| Beispiele: | |||||||||||||||||||||
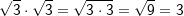 |
|||||||||||||||||||||
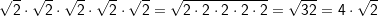 |
|||||||||||||||||||||
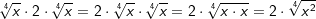 |
|||||||||||||||||||||
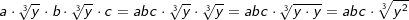 |
|||||||||||||||||||||
Ungleichnamige Wurzeln multiplizieren
| Wurzeln mit ungleichen Wurzelexponenten müssen vor ihrer Multiplikation durch geeignete Umformung auf den gleichen Wurzelexponenten gebracht werden, wie nachfolgendes Beispiel zeigt: | |||||||||||||||||||||
| Beispiel: | |||||||||||||||||||||
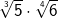 |
|||||||||||||||||||||
| Bestimmung des kgV der Wurzelexponenten. Der kgV von 3 und 4 ist 12. Erweiterung der Wurzelexponenten auf den kgV: |
|||||||||||||||||||||
 |
|||||||||||||||||||||
| Wurzeln multiplizieren | |||||||||||||||||||||
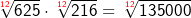 |
|||||||||||||||||||||
| Die Multiplikation der Wurzelradikanten darf nicht negativ sein, wenn der Wurzelexponent gerade ist. (a∙b≥0). | |||||||||||||||||||||
Merksatz Multiplikation von ungleichnamigen Wurzeln
|
|||||||||||||||||||||
| Beispiele: | |||||||||||||||||||||
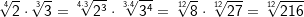 |
|||||||||||||||||||||
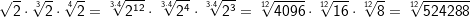 |
|||||||||||||||||||||
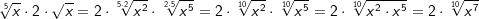 |
|||||||||||||||||||||
 |
|||||||||||||||||||||
Division von Wurzeln
Gleichnamige Wurzeln dividieren
| Es können nur Wurzeln mit gleichem Wurzelexponenten dividiert werden. Es gibt dabei eine Einschränkung: | |||||||||||||||||||||
| • | Ist der Wurzelexponent gerade, darf die Division der Wurzelradikanten nicht negativ sein. (a : b ≥ 0; b≠0). | ||||||||||||||||||||
Merksatz Division von gleichnamigen Wurzeln
|
|||||||||||||||||||||
| Beispiele: | |||||||||||||||||||||
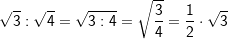 |
|||||||||||||||||||||
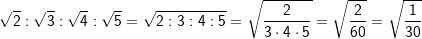 |
|||||||||||||||||||||
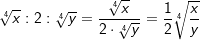 |
|||||||||||||||||||||
 |
|||||||||||||||||||||
Ungleichnamige Wurzeln dividieren
| Wurzeln mit ungleichen Wurzelexponenten müssen vor ihrer Division durch geeignete Umformung auf den gleichen Wurzelexponenten gebracht werden, wie folgendes Beispiel zeigt: | |||||||||||||||||||||
| Beispiel: | |||||||||||||||||||||
 |
|||||||||||||||||||||
| Bestimmung des kgV der Wurzelexponenten. Der kgV von 3 und 4 ist 12. Erweiterung der Wurzelexponenten auf den kgV: |
|||||||||||||||||||||
 |
|||||||||||||||||||||
| Wurzeln dividieren | |||||||||||||||||||||
 |
|||||||||||||||||||||
| Die Division der Wurzelradikanten darf nicht negativ sein, wenn der Wurzelexponent gerade ist. (a:b≥0; b≠0). | |||||||||||||||||||||
Merksatz Division von ungleichnamigen Wurzeln
|
|||||||||||||||||||||
| Beispiele: | |||||||||||||||||||||
 |
|||||||||||||||||||||
 |
|||||||||||||||||||||
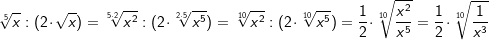 |
|||||||||||||||||||||
 |
|||||||||||||||||||||
| Multiplikation und Division von Wurzeln Level 1 / Blatt 1 33 Aufgaben im Blatt |
| Multiplikation und Division von Wurzeln Level 1 / Blatt 2 32 Aufgaben im Blatt |
| Multiplikation und Division von Wurzeln Level 2 / Blatt 1 10 Aufgaben im Blatt |
| Multiplikation und Division von Wurzeln Level 2 / Blatt 2 15 Aufgaben im Blatt |
| Multiplikation und Division von Wurzeln Level 2 / Blatt 3 22 Aufgaben im Blatt |
| Du befindest dich hier: |
| WIKI zur Multiplikation und Division von Wurzeln |