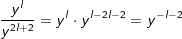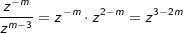 |
|
Potenzrechnung - Potenzterme vereinfachen |
|
Video zur Übersicht über die Potenzgesetze
Tipps und Tricks zu Potenzterme vereinfachen
| Unter 'Potenzterme vereinfachen' verstehen wir einen komplexen Rechenausdruck, der aus verschiedenen mathematischen Operationen zusammengesetzt ist (Addition, Subtraktion, Multiplikation, Division, Potenzieren, Wurzelziehen und andere mehr). Mit entsprechenden Rechengesetzen ist es möglich, diesen Ausdruck in eine einfachere Form zu bringen. Wir benötigen zur Vereinfachung eine bestimmte Vorgehensweise, die wir nun anhand von vier Beispielen kennenlernen wollen. Es sind aber nur Beispiele, es gibt noch viel mehr Vereinfachungsmöglichkeiten als in den Beispielen angeführt. Deshalb solltest du die Aufgaben dieses Kapitels intensiv üben, denn Mathematik lernt man nur durch Üben. |
Beispiel 1
Vereinfache den Term 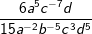 so weit wie möglich.1. Schritt: Findest du Zahlen im Ausdruck, so kürze diese zuerst, falls möglich.  |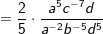
| 2. Schritt: Untersuche den Term auf Exponenten mit gleicher Basis und vereinfache nach den Potenzregeln, hier im Beispiel zunächst die Exponenten zur Basis a, denn  . |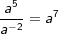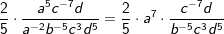
| 3. Schritt: Schritt für Schritt folgen die anderen Exponenten mit gleicher Basis. b ist alleine mit  ,  ,  . |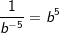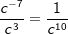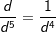
| 4. Schritt: Der vereinfachte Ausdruck lautet nun  . |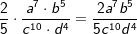
Beispiel 2
| Häufig sind in Exponenten auch Variable enthalten, wie z. B. im Ausdruck 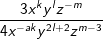 . Auch hier gehen wir schrittweise vor und zwar zu den Exponenten mit gleicher Basis.1. Schritt: Findest du Zahlen im Ausdruck, so kürze diese zuerst, falls möglich. Da sich  nicht kürzen lässt, bleibt es bei . |
|||||
| 2. Schritt: Untersuche den Term auf Exponenten mit gleicher Basis und vereinfache nach den Potenzregeln, hier im Beispiel zunächst die Exponenten zur Basis x, denn 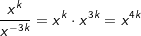 .3. Schritt: Schritt für Schritt folgen die anderen Exponenten mit gleicher Basis. |
|||||
|
|||||
| 4. Schritt: Der vereinfachte Ausdruck lautet nun  . |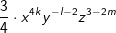
Beispiel 3
Wenn du einen Bruch mit einem negativen Exponenten findest, wie z. B.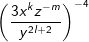 , mache aus dem negativen Exponenten einen positivenExponenten, indem du einfach den Kehrwert des Bruches bildest, denn  . |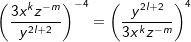
Beispiel 4
Wenn du die Division zweier Brüche findest. wie z. B.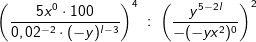 , dann denke daran, dass Brüche dividiertwerden, indem mit dem Kehrwert des zweiten Bruchs multipliziert wird.  |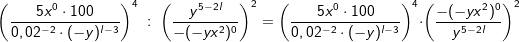
Prüfe dein Expertenwissen
| Wenn du die Aufgaben in den Arbeitsblättern der drei Level „Grundlagen“, „Fortgeschritten“ und „Expert“ erfolgreich lösen konntest und damit ein allumfassendes Wissen der Potenzregeln erworben hast, solltest du nun dein Expertenwissen prüfen. Die Aufgaben im Kapitel „Universität“ sind komplexer Natur und verlangen absolutes Wissen über alle Regeln der Potenzrechnung. Wenn du mindestens 30 der 37 Aufgaben (Arbeitsblätter 1, 2 und 3) fehlerfrei lösen kannst, ist dir die 1 in der Mathearbeit über Potenzrechnung sicher. |
Potenzterme vereinfachen Aufgabenblatt Level 1 / Blatt 1  73 Aufgaben im Blatt |
| Potenzterme vereinfachen Aufgabenblatt Level 2 / Blatt 1 54 Aufgaben im Blatt |
| Potenzterme vereinfachen Aufgabenblatt Level 2 / Blatt 2 53 Aufgaben im Blatt |
| Potenzterme vereinfachen Aufgabenblatt Level 3 / Blatt 1 12 Aufgaben im Blatt |
| Potenzterme vereinfachen Aufgabenblatt Level 3 / Blatt 2 20 Aufgaben im Blatt |
| Potenzterme vereinfachen Aufgabenblatt Level 4 / Blatt 1 12 Aufgaben im Blatt |
| Potenzterme vereinfachen Aufgabenblatt Level 4 / Blatt 2 13 Aufgaben im Blatt |
| Potenzterme vereinfachen Aufgabenblatt Level 4 / Blatt 3 12 Aufgaben im Blatt |
