 |
|
WIKI zu Potenzen mit rationalem Exponenten |
|


Potenzen mit rationalem Exponenten Einleitung
| Zwei Schüler unterhalten sich: |
 „Max, stimmt es eigentlich, dass Exponenten auch als Brüche existieren?“ „Max, stimmt es eigentlich, dass Exponenten auch als Brüche existieren?“„Ja, das soll es geben“, antwortet Peter, „ich weiß nur nicht, wie das gehen soll, dass man eine Zahl z. B. ein halb mal mit sich selbst multipliziert.“ Alles Mögliche haben wir nun schon mit Potenzen angestellt. Wir haben sie addiert, subtrahiert, multipliziert, dividiert und potenziert. Aber bei allen Operationen hatten wir immer eine ganze Zahl als Exponenten, sowohl ganze positive als auch negative Zahlen, ja, es war sogar die Null dabei. In diesem Kapitel haben wir es nun mit Aufgaben zu tun, in denen die Hochzahl auch eine rationale Zahl sein kann. Wir erinnern uns an ein paar Schuljahre zurück, wo wir uns mit der Bruchrechnung beschäftigten. Dort haben wir gelernt, dass man jeden beliebigen Bruch bzw. Dezimalzahlen mit endlichen bzw. periodisch wiederkehrenden Nachkommastellen der Menge der |
| rationalen Zahlen |
zuordnet. Wir haben sogar das mathematische Zeichen hierfür kennengelernt. Die Gesamtmenge der rationalen Zahlen bezeichnen wir mit 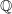 . .Eine rationale Zahl ist nichts anderes als ein Bruch, bei dem der Zähler als auch der Nenner wiederum aus einer ganzen Zahl besteht. Somit ist eine rationale Zahl. |
Beispiele zu rationalen Zahlen
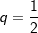 |
ist eine rationale Zahl bestehend aus den natürlichen Zahlen 1 und 2 im Zähler bzw. Nenner. Da du 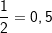 schreiben kannst, ist die Zahl 0,5 auch eine rationale Zahl. schreiben kannst, ist die Zahl 0,5 auch eine rationale Zahl. |
|
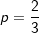 |
ist eine rationale Zahl bestehend aus den natürlichen 2 und 3 im Zähler bzw. Nenner. Da du 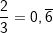 schreiben kannst, ist die Zahl schreiben kannst, ist die Zahl 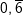 auch eine rationale Zahl. auch eine rationale Zahl. |
|
| ABER: | ||
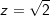 |
ist keine rationale Zahl, denn 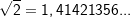 , die Anzahl der Nachkommastellen ist weder endlich noch periodisch wiederkehrend. , die Anzahl der Nachkommastellen ist weder endlich noch periodisch wiederkehrend. |
Regeln und Beispiele zu Potenzen mit rationalem Exponenten
Die Syntax
| Potenzen mit rationalem Exponenten haben die Form |
Potenzdarstellung von Wurzeln
Potenzen mit rationalem Exponenten werden als eine andere Schreibweise für Wurzeln verwendet. Genaueres hierüber findest du im Kapitel „Potenzdarstellung von Wurzeln“. In diesem Kapitel geben wir dir deshalb lediglich eine Kurzfassung dieser Darstellung. Es gilt: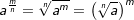 mit mit 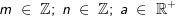 mit m als ganzer Zahl, n als natürlicher Zahl und a als jeder beliebigen reellen Zahl ≥ 0. Wie du aus der allgemeinen Schreibweise erkennst, wird der Zähler m des rationalen Exponenten zum ganzzahligen Exponenten der Basis a. Der Nenner n des rationalen Exponenten wird zum Exponenten der Wurzel. |
Beispiele 1 und 2
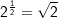 |
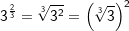 |
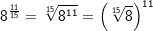 |
|
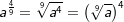 |
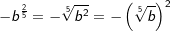 |
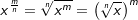 |
Video zur Potenzdarstellung von Wurzeln (Laufzeit ca. 6 Minuten)
Rechenregeln
| Die Rechenregeln für Potenzen mit rationalem Exponenten sind dieselben wie die für das Rechnen von Potenzen mit gleicher Basis und Potenzen mit gleichem Exponenten, also dem 1. Potenzgesetz , 2. Potenzgesetz , 3. Potenzgesetz und dem 4. Potenzgesetz. |
Beispiele 3, 4 und 5
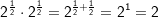 |
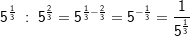 |
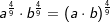 |
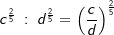 |
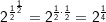 |
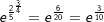 |
| Potenzen mit rationalem Exponenten Aufgabenblatt Level 1 / Blatt 1 176 Aufgaben im Blatt |
| Potenzen mit rationalem Exponenten Aufgabenblatt Level 1 / Blatt 2 176 Aufgaben im Blatt |
| Potenzen mit rationalem Exponenten Aufgabenblatt Level 1 /Blatt 3 176 Aufgaben im Blatt |
| Potenzen mit rationalem Exponenten Aufgabenblatt Level 1 /Blatt 4 176 Aufgaben im Blatt |
| Potenzen mit rationalem Exponenten Aufgabenblatt Level 2 / Blatt 1 45 Aufgaben im Blatt |
| Potenzen mit rationalem Exponenten Aufgabenblatt Level 2 / Blatt 2 47 Aufgaben im Blatt |
| Potenzen mit rationalem Exponenten Aufgabenblatt Level 2 / Blatt 3 58 Aufgaben im Blatt |
| Potenzen mit rationalem Exponenten Aufgabenblatt Level 2 / Blatt 4 92 Aufgaben im Blatt |
| Potenzen mit rationalem Exponenten Aufgabenblatt Level 3 / Blatt 1 128 Aufgaben im Blatt |
| Potenzen mit rationalem Exponenten Aufgabenblatt Level 3 / Blatt 2 128 Aufgaben im Blatt |
| Potenzen mit rationalem Exponenten Aufgabenblatt Level 3 / Blatt 3 89 Aufgaben im Blatt |



