 |
WIKI zu Logarithmus einer Zahl
|


Einführung
| Fangen wir als Einleitung zum Logarithmus einer Zahl doch gleich einmal mit einer Aufgabe an. Nachfolgend findest du Kärtchen mit Rechenoperationen von x, der Zahl 2 und der Zahl 16. Im letzten Kärtchen stehen nur Fragezeichen. |
||||
| x+2=16 x=16-2 |
2+x=16 x=16-2 |
|||
| x-2=16 x=16+2 |
2-x=16 x=2-16 |
|||
| x⋅2=16 x=16:2 |
2⋅x=16 x=16:2 |
|||
| x:2=16 x=16⋅2 |
2:x=16 x=2:16 |
|||
| x2=16 x=±√16 |
??? | |||
| Was meinst du gehört an die Stelle der Fragezeichen? | ||||
Die Syntax
| Sicher hast du bei den Kärtchen der Einleitung sofort erkannt, dass der Unterschied zwischen den Gleichungen lediglich darin besteht, dass der Platzhalter und die Zahl 2 ihre Plätze vertauscht haben. Also muss in das Kärtchen mit den Fragezeichen konsequenterweise die Gleichung |
| 2x=16 |
| folgen. Und mit dieser Gleichung, bei der die gesuchte Größe x als Exponent auftritt, kommen wir in Schwierigkeiten. Wie können wir diese Gleichung „nach x auflösen“, also so umformen, dass x alleine auf einer Seite steht? |
| 2x=16 |
| x=??? |
| Mit Worten können wir die gesuchte Zahl x ohne Schwierigkeiten beschreiben. x ist wohl diejenige Zahl mit der man die Zahl 2 potenzieren muss, um 16 zu erhalten. Auch können wir problemlos x durch ausprobieren ermitteln, den 2∙2∙2∙2=16=24. Folglich muss x wohl 4 sein. |
Diese Zahl x bezeichnen die Mathematiker als Logarithmus von 16 zur Basis 2 und schreiben dafür das Symbol |
| log2 (16). |
| Es gilt also: |
 |
| log2(16) ist „diejenige Zahl, mit der man 2 potenzieren muss, um 16 zu erhalten“. |
 |
| Und damit können wir das Kästchen mit den Fragezeichen komplettieren zu: |
| 2x=16 x=log2(16) |
Beispiel 1
Lösung 1
Beispiel 2
Lösung 2
Merksatz zum Logarithmus
| Es sei a>0; a≠1 die Basis einer Potenz und b>0 das Ergebnis der Potenz mit x, so bezeichnen wir die Lösung der Gleichung ax=b als den Logarithmus von b zur Basis a und schrieben dafür | |||
| x=loga(b). | |||
Die Äquivalenzumformung
| Mit der neuen Definition können wir unsere Ausgangsgleichung nach x auflösen. Wir erinnern uns daran, dass, wenn wir eine Gleichung verändern, diese Veränderung auf beiden Seiten des Gleichheitszeichens ausgeführt werden muss. Der Mathematiker nennt dies „Äquivalenzumformung“. | |||
| Das Bilden des Logarithmus bezeichnet man als Logarithmieren. Die Lösung einer Gleichung kann damit nun formal beschrieben werden mit | |||
| 2x=16 | Logarithmieren mit der Basis 2 | ||
| log2(2x)=log2(16) | |||
| x⋅log2(2)=log2(16) | |||
| Und wegen log2(2)=1 letztendlich | |||
| x=log2(16) | |||
| Viel haben wir damit allerdings nicht erreicht. Im Grunde genommen haben wir lediglich ein Symbol für die gesuchte Zahl eingeführt. Taucht nun die Frage auf, welche Zahl verbirgt sich hinter dem Symbol log2(16)? Vorläufig müssen wir uns dabei aufs Raten bzw. Ausprobieren verlegen. Durch geschicktes Probieren finden wir: |
|||
 |
|||
| log2(16)=4, denn 24=16 | |||
 |
|||
und haben damit nun endlich die Gleichung 2x=16 gelöst. Für ihre Lösungsmenge gilt 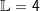 . . |
|||
| Und hier noch ein weiteres Beispiel: | |||
 |
|||
| log3(81)=4, denn 34=81 | |||
 |
|||
Lösungsmengen des Logarithmus
Zu den Lösungsmengen eines Logarithmus zählt die Menge der reellen Zahlen, wie nachfolgende Abschnitte zeigen (auf den komplexen Bereich wird in diesem Kapitel nicht eingegangen).
Positive ganze Zahlen oder 0
| In vielen Fällen ist der Logarithmus eine positive ganze Zahl oder 0, wie du an folgenden Beispielen erkennen kannst. |
Beispiel 3Lösung 3 |
Negative ganze Zahlen
| Wie die folgenden Beispiele zeigen, kann der Logarithmus jedoch durchaus auch eine negative ganze Zahl sein. |
Beispiel 4 |
Rationale Zahlen
| Dass der Logarithmus nicht nur ganzzahlig, sondern auch ein Bruch sein kann, zeigen dir die folgenden Beispiele: |
Beispiel 5 |
Irrationale Zahlen
| Als letzte der Zahlenmengen verbleiben noch die irrationalen Zahlen. Hierzu gehören alle Logarithmen, die weder ganzzahlig noch rational sind. Beispiele lassen sich hier nicht aufzeigen, da die Ergebnisse ja gerundet dargestellt werden müssten und damit das Ergebnis ein rationales Ergebnis wäre. So ist ja | |
| log13(7)=0,758654413……. | |
Lösungsmethoden des Logarithmus
| In vielen Fällen lässt sich das Ergebnis ohne großartige Berechnung sofort hinschreiben. Wenn es aber mal schwieriger wird, dann empfiehlt es sich, zur Potenzschreibweise überzugehen. |
Potenzschreibweise
| Mit Hilfe der Potenzschreibweise kann man erreichen, dass beiderseits des Gleichheitszeichens die gleiche Basis steht. Der gesuchte Logarithmus ergibt sich dann aus dem Exponenten-Vergleich. |
Beispiel 6Beispiel 7 |
Berechnung der Basis, des Numerus und des Logarithmuswertes
| In den bisherigen Beispielen war stets die Basis a und der Numerus b gegeben. Gesucht wurde der Logarithmuswert c. Natürlich können wir aber auch die Basis ermitteln, wenn der Numerus und der Logarithmuswert gegeben sind. |
Beispiel 8Beispiel 9 |
| In den folgenden Beispielen sind Basis und Logarithmuswert gegeben, zu bestimmen ist der Numerus. Dies ist besonders einfach, wenn wir zur Potenzschreibweise übergehen. |
Beispiel 10Beispiel 11Beispiel 12 |
Logarithmus Sonderregeln
Es existieren drei besondere Regeln, die du auswendig lernen solltest:
1. Sonderregel

Jeder Logarithmus von seiner Basis ist immer 1.
2. Sonderregel

Jeder Logarithmus von 1 ist stets 0.
3. Sonderregel
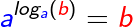
Logarithmen als Potenz ihrer Basis heben sich auf.
1. Sonderregel

Jeder Logarithmus von seiner Basis ist immer 1.
2. Sonderregel

Jeder Logarithmus von 1 ist stets 0.
3. Sonderregel
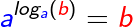
Logarithmen als Potenz ihrer Basis heben sich auf.
| Logarithmus einer Zahl Level 1 / Blatt 1 26 Aufgaben im Blatt |
| Logarithmus einer Zahl Level 1 / Blatt 2 36 Aufgaben im Blatt |
| Logarithmus einer Zahl Level 1 / Blatt 3 40 Aufgaben im Blatt |
| Logarithmus einer Zahl Level 2 / Blatt 1 39 Aufgaben im Blatt |
| Logarithmus einer Zahl Level 2 / Blatt 2 39 Aufgaben im Blatt |
| Logarithmus einer Zahl Level 2 / Blatt 3 66 Aufgaben im Blatt |
| Du befindest dich hier: |
| WIKI zu Logarithmus einer Zahl |



