 |
WIKI zur Logarithmenberechnung
|


Einführung
| Bisher haben wir den Logarithmus einer Zahl nur durch Probieren gefunden. Dementsprechend waren auch alle Beispiele und Aufgaben so gewählt, dass man durch geschicktes Probieren zum Ziel gelangen konnte. Zum Beispiel: | |||
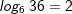 denn denn 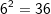 |
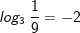 denn denn 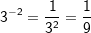 |
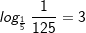 denn denn 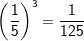 |
|
| Was machen wir aber, wenn beispielsweise nach folgenden Logarithmen gefragt wird: | |||
| • | log6 30=???? | ||
| • | log2 3=???? | ||
| • | log10 48=???? | ||
| Mit Probieren kommen wir in diese Fällen nicht weiter, weil diese Logarithmen irrationale Zahlen sind, von denen man nur rationale Näherungswerte bestimmen kann. Bereits Anfang des Jahrhunderts machten sich einige Mathematiker mit unvorstellbarem Fleiß an die undankbare aber wichtige Arbeit, Tausende und Abertausende von Logarithmen zu berechnen und in „Logarithmentafeln“ zusammenzustellen. Die Schwierigkeit dabei war allerdings, dass man eine Auswahl treffen musste, denn zum einen gibt es ja unendlich viele Logarithmen und zum anderen unendlich viele Basen, weil ja jede positive von eins verschiedene Zahl als Basis in Frage kommt. Alle Logarithmen zu ein und derselben Basis fasst man zu einem sogenannten „Logarithmensystem“ zusammen. Der Not der unendlich vielen Logarithmensysteme gehorchend, haben Mathematiker sich der Erstellung von Logarithmentafeln des dekadischen Logarithmus (Logarithmus zur Basis 10) beschränkt, gleichzeitig aber einen Weg gesucht, wie man aus dem dekadischen Logarithmus alle anderen Logarithmen zu einer beliebigen Basis berechnen kann. Mit dem Aufkommen elektronischer Taschenrechner haben sich die Logarithmentafeln überholt. Heute kann jeder beliebige Logarithmus zu jeder beliebigen Basis schnell und ohne große Umstände direkt berechnet werden. Den Berechnungsmethoden mit einem wissenschaftlichen TR beschäftigen wir uns in diesem Kapitel. |
|||
Logarithmen mit einem Taschenrechner
| Auf wissenschaftlichen Taschenrechnern ab dem Jahre 1980 etwa befindet sich eine Taste mit der Aufschrift „log“. Diese Angabe „log“ steht für den dekadischen Logarithmus, also den Logarithmus zur Basis 10, kurz log geschrieben. Nun wollen wir wissen, welche Zahl denn log10 5 ist. Die nachfolgende Beschreibung entspricht dem WTR TI-30X Plus. Bei anderen Modellen muss gegebenenfalls eine andere Reihenfolge der Eingabe erfolgen. |
||
| 1. | Drücke die mit |
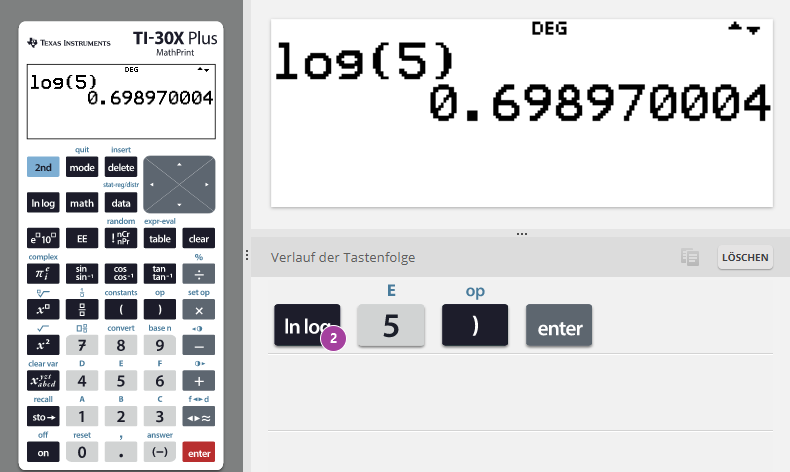 |
| 2. | Gebe eine 5 ein. | |
| 3. | Betätige die „)“-Taste. | |
| 4. | Betätige die „ENTER“-Taste. | |
| Das Ergebnis steht nun im Fenster. | ||
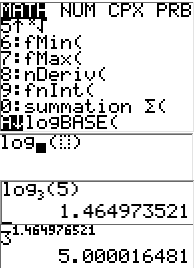
| Was müssen wir tun, wenn wir z. B. wissen wollen, was log3 5 ist? Nun, das hängt ganz davon ab, welchen Taschenrechner wir benutzen. Betrachten wir zunächst den einfachsten Fall, wir verwenden einen Taschenrechner, der auch eine andere Basis als 10 kennt. Die nachfolgende Grafik zeigt die Eingabe bei einem TI-84 PLUS. |
||
Im Menü  finden wir unter dem Punkt A: die Funktion „logBASE“. finden wir unter dem Punkt A: die Funktion „logBASE“. |
 |
||
| Wählen wir die an, erscheint das Eingabefenster. | |||
Als Basis geben wir die 3 ein und im Logarithmus-argument die Zahl 5 und betätigen mit  . Es erscheint das Ergebnis. . Es erscheint das Ergebnis. |
|||
| Wir machen noch die Probe mit 31,464976521 und erhalten korrekterweise das Ergebnis 5. | |||
| Wege und Schritte variieren, je nachdem von welchem Hersteller der TR ist. | |||
Logarithmen loga x mit a≠10 berechnen
| Entweder steht uns ein TR zur Verfügung, der auch andere Logarithmen als die zur Basis 10 berechnen kann (wie zuvor beschrieben), oder aber wir bedienen uns einer Umrechnung auf den Logarithmus zur Basis 10. Hierzu betrachten wir uns zunächst die Theorie. | |||
| Gesucht ist log3 x mit x > 0. Daraus folgt: | |||
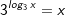 |
Logarithmieren zur Basis 10 | ||
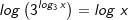 |
Anwendung von 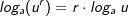 |
||
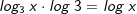 |
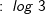 |
||
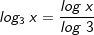 |
|||
| Wir haben somit einen Logarithmus zur Basis 3 auf den Logarithmus zur Basis 10 zurückgeführt. Jetzt können wir problemlos log3 5 lösen. | |||
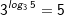 |
Logarithmieren zur Basis 10 | ||
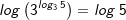 |
Anwendung von 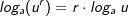 |
||
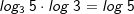 |
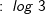 |
||
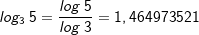 |
|||
| Damit können wir auch Logarithmen zu jeder beliebigen Basis lösen, auch wenn eine solche Operation auf dem eigenen TR nicht verfügbar ist. | |||
| Beispiele: | |||
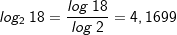 |
Probe: 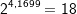 |
||
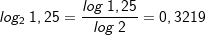 |
Probe: 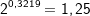 |
||
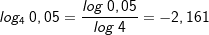 |
Probe: 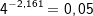 |
||
Verallgemeinerung der Beziehung loga x
Die Verallgemeinerung der Beziehung 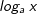 auf auf 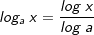 ist zwar eine Verallgemeinerung, aber noch nicht die Verallgemeinerung höchsten Grades, da wir mit ist zwar eine Verallgemeinerung, aber noch nicht die Verallgemeinerung höchsten Grades, da wir mit 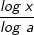 ja wieder auf einen speziellen Logarithmus zugreifen, nämlich dem Logarithmus zur Basis 10. Das ist zwar sinnvoll, da viele Taschenrechner genau diese Zehnerlogarithmen auf Knopfdruck liefern, es ist aber immer noch eine spezielle Beziehung. ja wieder auf einen speziellen Logarithmus zugreifen, nämlich dem Logarithmus zur Basis 10. Das ist zwar sinnvoll, da viele Taschenrechner genau diese Zehnerlogarithmen auf Knopfdruck liefern, es ist aber immer noch eine spezielle Beziehung. |
| Wollen wir vollständig verallgemeinern müssen wir schreiben: |
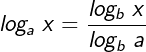 mit mit 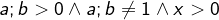 |
| Diese Gleichung beschreibt den Zusammenhang zweier beliebiger Logarithmensysteme. Wenn auch diese Beziehung für uns kaum von praktischer Bedeutung ist, muss sie der Vollständigkeit halber erwähnt werden. |
| Berechnung von Logarithmen Aufgabenblatt 1 24 Aufgaben im Blatt |
| Berechnung von Logarithmen Aufgabenblatt 2 29 Aufgaben im Blatt |
| Du befindest dich hier: |
| WIKI zur Logarithmenberechnung |



