 |
WIKI zu logarithmischen Gleichungen |
Einführung
| Mit der Beziehung loga b=c lassen sich, – ähnlich der Prozentrechnung – drei verschiedene Arten von Bestimmungsgleichungen aufstellen, und zwar: | ||||
| 1. Art | 2. Art | 3. Art | ||
| Die Frage nach dem Logarithmuswert führt auf eine Gleichung der Form | Die Frage nach der Basis führt auf eine Gleichung der Form | Die Frage nach dem Numerus führt auf eine Gleichung der Form | ||
| loga b=x | logx b=c | loga x=c | ||
| log2 16=x | logx 9=2 | log5 x=4 | ||
| Bei Gleichungen der 1. Art kann für x grundsätzlich jede reelle Zahl stehen, weil Logarithmen jede reelle Zahl annehmen können. | Bei Gleichungen der 2. Art können für x nur positive reelle Zahlen ungleich 1 stehen, weil die Basis eines Logarithmus stets positiv und ungleich 1 sein muss. | Bei Gleichungen der 3. Art können für x nur positive reelle Zahlen stehen, weil der Logarithmus nur von positiven Zahlen gebildet werden kann. | ||
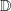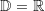Die Definitionsmenge  der Gleichung loga b=x ist also die Menge der reellen Zahlen: Gleichungen der 1. Art sind praktisch schon nach x aufgelöst. |
Die Definitionsmenge 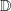der Gleichung logx b=c ist also die Menge der positiven reellen Zahlen ohne 1: 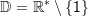 Gleichungen der 2. Art führen auf eine Gleichung der Form |
Die Definitionsmenge 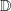der Gleichung loga x=c ist also die Menge der positiven reellen Zahlen 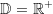 Gleichungen der 3. Art führen auf eine Gleichung der Form |
||
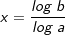 x=log2 16 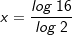 x = 4 |
xb=c logx 9=2 x2 = 9 x1 = 3 x2 = -3 |
x=ac log5 x=4 x = 54 x = 625 |
||
| Da 4 in der Definitions-menge enthalten ist, gilt für die Lösungsmenge: | Da -3 in der Definitions-menge nicht enthalten ist, gilt für die Lösungsmenge: | Da 625 in der Definitions-menge enthalten ist, gilt für die Lösungsmenge: | ||
 . |
 . |
 . |
||
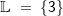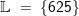Logarithmische Gleichungen lösen
| Im Folgenden werden wir uns hauptsächlich mit Bestimmungsgleichungen beschäftigen, die im weitesten Sinne zur 3. Art gehören, wie beispielsweise | |||
| • | log3(3x+5)=5 | • | log2 (x2-1)=3 |
| • | log x+log 3=log 5 | • | log5 (2x+6)-log5 (x+3)=2 |
| • | 2⋅log3 x =log3 (x+6) |
• | log2 x+log2 5=1+log2 (1+x2) |
| Allen diesen Bestimmungsgleichungen gemeinsam ist, dass sie die Unbekannte x im Numerus von Logarithmen enthalten. Derartige Gleichungen bezeichnen wir als logarithmische Gleichungen. | |||
| Das Lösen logarithmischer Gleichungen erfolgt in 4 Schritten. | |||
| 1. Schritt: | |||
| Da der Numerus eines Logarithmus nicht negativ werden kann, müssen wir zunächst die Definitionsmenge aufstellen, also ausschließen, für welche Werte von x die Gleichung keine Lösung hat. | |||
| 2. Schritt: | |||
| Wir Entlogarithmieren, d.h., wir potenzieren beide Seiten der Gleichung mit der Basis des Logarithmus. Anschließend lösen wir die Gleichung entsprechend den Äquivalenzregeln nach x auf. | |||
| 3. Schritt: | |||
| Wir schreiben die Lösungsmenge auf, prüfen zuvor jedoch, ob eventuell ein x-Wert über die Definitionsmenge ausgeschlossen ist. | |||
| 4. Schritt: | |||
| Wir setzen den / die gefundenen x-Werte in die Ausgangsgleichung ein und machen die Probe. | |||
| Wir betrachten uns die nachfolgenden | |||
Beispiele
Beispiel 1
Beispiel 2
Beispiel 3
Beispiel 4
Logarithmische Gleichungen mit mehr als einem Logarithmus
| Häufig treten in einer logarithmischen Gleichung zwei oder mehrere Logarithmen auf. In diesem Falle müssen wir mithilfe der Logarithmengesetze die Logarithmen zu einem einzigen Logarithmus zusammenfassen. |
Beispiel 5
Fehlerentstehung bei logarithmischen Gleichungen
| Beim Zusammenfassen von mehreren Logarithmen zu einem Logarithmusausdruck können mathematische Fehler entstehen, dergestalt, dass sich falsche Lösungsmengen einschleichen. Hierzu betrachten wir folgendes Beispiel: |
Beispiele
Beispiel 6
| Wir sehen unmittelbar, dass x=-10 keine Lösung der logarithmischen Gleichung sein kann, denn wenn wir diesen Wert in die Ausgangsgleichung einsetzen würden, bekämen wir ein negatives Logarithmusargument (log(-10)). Es gibt aber keine Logarithmen von negativen Zahlen. Die Lösung x=-10 hat sich somit durch die Anwendung der Logarithmusgesetze eingeschlichen. Wir fragen uns, warum. Gleichungen, die dieselbe Lösungsmenge haben, bezeichnen wir als äquivalente Gleichungen. Äquivalent sind z. B. die beiden Gleichungen 3x+2=8 und 3x=6, denn beide haben dieselbe Lösungsmenge  . |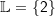
||
| Ändert sich bei der Umformung einer Gleichung die Lösungsmenge nicht, dann spricht man von einer Äquivalenzumformung. Zu den Äquivalenzumformungen gehören: |
||
| • | die Addition derselben Zahl auf beiden Seiten der Gleichung. | |
| • | die Subtraktion derselben Zahl von beiden Seiten der Gleichung. | |
| • | die Multiplikation beider Seiten einer Gleichung mit derselben von Null verschiedenen Zahl. | |
| • | die Division beider Seiten einer Gleichung durch dieselbe von Null verschiedene Zahl. | |
| Die Anwendung der Logarithmengesetze zählt nicht zu den Äquivalenzumformungen, da sich dabei die Lösungsmenge ändern kann. | ||
| Wie jedoch können wir dieses Problem bei der Behandlung logarithmischer Gleichungen umgehen? |  Gleich zu Beginn der Gleichungslösung die Definitionsmenge aufstellen. |
|
| Und zur Warnung gleich noch zwei Beispiele in verkürzter Form. | ||
Beispiel 7
Beispiel 8
Lösungsmethoden logarithmischer Gleichungen
| Neben den bislang behandelten Lösungsmethoden können zusätzliche Wege zu einer schnellen Lösung führen, ohne dass umständlich entlogarithmiert werden muss. |
Logarithmische Gleichungen in der Form loga(u)=loga(v)
| Besonders leicht zu lösen sind logarithmische Gleichungen, bei denen rechts und links des Gleichheitszeichens nur je ein Logarithmus zur gleichen Basis steht. |
| Sind nämlich die Logarithmen zweier positiver Zahlen u und v gleich, dann sind auch die beiden Zahlen u und v selbst gleich und es gilt folgender Merksatz: |
Auf Grund dieser Gesetzmäßigkeit lässt sich beispielsweise die logarithmische Gleichung log5(x+7)=log5(2x-3) mit 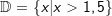 problemlos in eine logarithmenfreie Form bringen. |
Beispiel 9
| Enthält die Gleichung mehr als zwei Logarithmen, dann fasst man diese unter Verwendung der Logarithmengesetze so zusammen, dass schließlich rechts und links vom Gleichheitszeichen nur noch je ein Logarithmus steht. |
Beispiel 10
Logarithmische Gleichungen mittels Substitution lösen
| Gelegentlich begegnen wir auch logarithmischen Gleichungen, bei denen die zweite Potenz, also das Quadrat eines Logarithmus, auftritt. Bei derartigen Aufgaben bedienen wir uns der Substitution. |
Beispiel 11
| Wenn die Numeri der auftretenden Logarithmen nicht gleich sind, dann versagt das zuvor beschrieben Verfahren. Manchmal kommt man aber trotzdem weiter, wenn man geschickte Umformungen nach den Logarithmusgesetzen vornimmt. |
Beispiel 12
Logarithmische Gleichungen mit versteckter Potenz
| Manchmal gibt eine logarithmische Gleichung nicht sofort zu erkennen, dass sie das Quadrat eines Logarithmus enthält. Da müssen wir dann erst genauer hinschauen und die ein oder andere Umformung vornehmen. |
Beispiel 13
Logarithmische Gleichungen Aufgabenblatt Level 1/ Blatt 1  18 Aufgaben im Blatt |
| Logarithmische Gleichungen Aufgabenblatt Level 1 / Blatt 2 18 Aufgaben im Blatt |
| Logarithmische Gleichungen Aufgabenblatt Level 2 / Blatt 1 18 Aufgaben im Blatt |
| Logarithmische Gleichungen Aufgabenblatt Level 2 / Blatt 2 18 Aufgaben im Blatt |
| Logarithmische Gleichungen Aufgabenblatt Level 3 / Blatt 1 10 Aufgaben im Blatt |
| Logarithmische Gleichungen Aufgabenblatt Level 3 / Blatt 2 12 Aufgaben im Blatt |
| Logarithmische Gleichungen Aufgabenblatt Level 3 / Blatt 3 12 Aufgaben im Blatt |
| Du befindest dich hier: |
| WIKI zu logarithmischen Gleichungen |
