Integrationsregeln Basis

Unbestimmtes Integral / Integrationsregeln Basis

Nachfolgend sind die Basisregeln der Integration im einzelnen aufgeführt. Die hier aufgeführten Regeln entsprechen dem Lehrumfang der Gymnasien G8 und G9 in der BRD.
Weitere Integrationsregeln im Kapitel "Integrationsregeln komplex".

Die Nullregel

Die Nullregel besagt, dass das Integral von Null eine Konstante ist.

$Fit in Mathe Latex: d68ebe277ebe46af4d69cc2e1b37f66a.png$

Die 1-Regel

Die 1-Regel besagt, dass das Integral von 1 x ist.

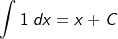$Fit in Mathe Latex: 9c1e29f1fc2846a4d067407f83cb6292.png$

Die Konstantenregel

Die Konstantenregel besagt, dass eine Konstante $Fit in Mathe Latex: a07cc6fe2105c06dfb45c16ddacced8c.png$ zum Faktor der Stammfunktion wird.

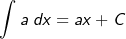$Fit in Mathe Latex: c0c9f4ae55206c99f6ff934d887ec65a.png$

Die Potenzregel

Die Potenzregel lautet:

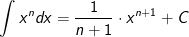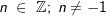$Fit in Mathe Latex: 1e59312ea290f406e4399dd117450224.png$ mit $Fit in Mathe Latex: a3703d1a360a313ce17814c6501b766d.png$ und zusätzlich $Fit in Mathe Latex: e5da5dbe32b35638dd38d49e22b96db8.png$ falls n<-1.

An dieser Stelle erkennen wir gut die Umkehrrechenart. Wird bei der Potenzregel der Ableitung die Hochzahl als Faktor vor den Term geschrieben und anschließend um den Wert 1 vermindert, so wird bei der Potenzregel der Integration die Hochzahl um 1 erhöht und diese neue Hochzahl in den Nenner eines Bruchs geschrieben.

Beispiel 1

Bilde alle Stammfunktionen F der Funktion 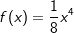$Fit in Mathe Latex: 3d34644d9d5fe8abc99ca53673fc884b.png$ .

Lösung 1

Beispiel 2

Bilde alle Stammfunktionen F der Funktion f(x)=x⁵ +x³.

Lösung 2

Die erweiterte Potenzregel

Für die Potenzfunktion f(x)=x^q mit 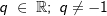$Fit in Mathe Latex: 889c6c3448978e3486d31da1d9502720.png$ und x>0 gilt:

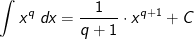$Fit in Mathe Latex: 66f1031b338d79934cbdb18b056f762c.png$

Die erweiterte Potenzregel entspricht der zuvor beschriebenen Potenzregel 1:1 mit der Erweiterung, dass der Exponent nicht mehr Element der ganzen Zahlen ist, sonder Element der rationalen Zahlen.

Beispiel 3

Bilde alle Stammfunktionen F der Funktion 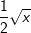$Fit in Mathe Latex: 184cd45cdf267bfd1d366d999e22e91e.png$ .

Lösung 3

Beispiel 4

Bilde alle Stammfunktionen F der Funktion 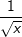$Fit in Mathe Latex: f7d2b2ed8715eee474bd87afee9fb582.png$ .

Lösung 4

Die Faktorregel

Die Faktorregel besagt, dass Faktoren erhalten bleiben. Es sei f eine in ganz 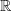$Fit in Mathe Latex: a5b7a189c728560bdaf3713d33b15508.png$ differenzierbare Funktion. Dann gilt:

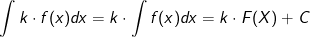$Fit in Mathe Latex: c2b8dad7afd6ca6d31d7808a413847ea.png$ .

Dies entspricht der Faktorregel der Ableitungen.

Die Summen- bzw. Differenzregel

Es seien f und g stetige Funktionen. Dann gilt:

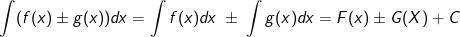$Fit in Mathe Latex: c2c5d020dac307b7ec4cd989c1a1d3a4.png$

Bei zusammengesetzten Funktionen werden die Summanden / Subtrahenden einzeln integriert. Dies entspricht ebenfalls der Summen- bzw. Differenzregel der Ableitungen.

Beispiel 5

Bilde alle Stammfunktionen F der Funktion f(x)=3sin(x)-2cos(x).

Lösung 5

Lineare Substitution

Es sei f eine verkettete Funktion mit f(x)=v(u(x)) und u(x)=z eine lineare Funktion in der Form z=ax+b sowie F eine Stammfunktion der äußeren Funktion v, dann gilt:

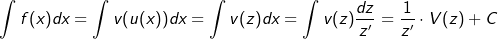$Fit in Mathe Latex: f38f12e3c6162f7f91b7033ec02e23b2.png$

zugegebener Maßen ein kompliziert zu verstehender Ausdruck.

Für den mathematisch Interessierten:

Beweis:

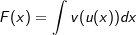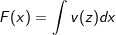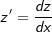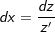Es sei f(x)=v(u(x)). Dann ist die Stammfunktion $Fit in Mathe Latex: 48506214f841214d47d58450dd82e054.png$ . Wir substitieren z=u(x) dann ist $Fit in Mathe Latex: d21eb312f1c990fef9714dce0445a5fd.png$ . Nun bilden wir $Fit in Mathe Latex: 3d16411f88cb1774f0c9481778a34605.png$ . Diesen Ausdruck stellen wir um nach dx: $Fit in Mathe Latex: 07b72b669d24ea0c2f5eff517e96f68d.png$ . 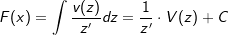Jetzt ersetzen wir dx im Integral durch diesen Ausruck und erhalten $Fit in Mathe Latex: 328973649de2c9a075278f4350f8b777.png$

Beispiel 6

Bilde eine Stammfunktionen F der Funktion f(x)=(2x-5)².

Lösung 6

Für den mathematischen Praktiker:

Bei der linearen Substition (ein viel zu kompliziertes Wort) wird die Stammfunktion gebildet durch:

Integration der äußeren Funktion dividiert durch die Ableitung der inneren Funktion.

Beispiel 7

Bilde eine Stammfunktionen F der Funktion 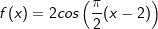$Fit in Mathe Latex: 77def6e2b4e0dcc9eaf74043a961b394.png$ .

Lösung 7

Wir merken uns die Vorgehensweise:
1.	Schreibe einen Bruchstrich.
2.	Bilde die Stammfunktion der äußeren Funktion und schreibe diese in den Zähler des Bruchs.
3.	Bilde die Ableitung der inneren (linearen) Funktion und schreibe diese in den Nenner des Bruchs.
4.	Vereinfache so weit wie möglich.

Formansatz mit Koeffizientenvergleich

In einigen Bundesländern (z. B. Hessen) wird bezüglich der Integration von e-Funktionen der Formansatz mit Koeffizientenvergleich gelehrt. Dieses Verfahren ersetzt für diesen speziellen Bereich die partielle Integration, wie Letztere im Kapitel „Integrationsregeln komplex“ beschrieben ist.

Ausgehend von einer aus ganzrationaler und Exponentialfunktion zusammengesetzten Funktion als Ableitungsfunktion wird über einen Formansatz eine allgemeine Lösung der Stammfunktion gebildet. Diese Stammfunktion wird abgeleitet und mit der gegebenen Ableitungsfunktion verglichen.

Es sei f(x)=(2x-1)∙e^2x die gegebene Ableitungsfunktion. Der Formansatz der gegebenen Stammfunktion lautet nun F(x)=(Ax+B)∙e^2x. Die Stammfunktion wird nun abgeleitet und die sich ergebenden Koeffizienten A und B mit der Ableitungsfunktion verglichen. Dabei ergibt sich in der Regel ein lineares Gleichungssystem.

Beispiel 8

Bilde eine Stammfunktionen F der Funktion f(x)=(2x-1)∙e^2x mithilfe eines Formansatzes mit Koeffizientenvergleich.

Lösung 8

Beispiel 9

Bilde eine Stammfunktionen F der Funktion f(x)=(x²-2x)∙e^-0,5x mithilfe eines Formansatzes mit Koeffizientenvergleich.

WIKI unbestimmtes Integral - Integrationsregeln Basis