 |
WIKI zur Kapitalentwicklung mit Zinseszinsen
|
Kapitalentwicklung mit Zinseszinsen
| Im Kapitel Zinseszinsen haben wir die Berechnungsformel für die Zinseszinsrechnung kennengelernt. In diesem Kapitel beschäftigen wir uns nun mit der Kapitalentwicklung innerhalb der Zinseszinsrechnung. |
| Unter „Kapitalentwicklung“ verstehen wir die einmalige Einzahlung eines bestimmten Betrages – des Anfangskapitals K0 - bei einer Bank für einen Zeitraum von mindestens einem Jahr. Wir wollen wissen, wie sich dieses eingezahlte Kapital „entwickelt“ und mit welchem Betrag - Endkapital Kn - wir nach Ablauf von n Jahren bei einem Zinssatz von p% rechnen können. |
Die Zinseszinsformel für festen Zinssatz
| Die Zinseszinsformel für festen Zinssatz lautet | |
 |
|
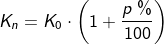| und mit | |
 , |
|
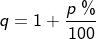| vereinfacht zu: | |
 . |
|
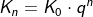| In der Formel bedeutet: | |
| K0 = | Anfangskapital |
| Dies ist der Geldbetrag, den wir zur Bank bringen und anlegen, es ist aber auch gleichzeitig der Geldbetrag, den wir bei einer Bank ausleihen, weil wir einen Kredit benötigen. | |
| Kn = | Endkapital |
| Dies ist der Geldbetrag, den wir nach n Jahren auf unserem Konto zur Verfügung haben, wenn unser Anfangskapital n Jahre lang mit p % Zinsen verzinst wurde. | |
| p% = | Zinssatz |
| Dies ist der Prozentsatz, mit dem unser Anfangskapital Jahr für Jahr einschließlich Zinsen verzinst wird. | |
| n = | Anzahl der Jahre |
| Dies sind die Anzahl Jahre, die wir das Geld auf der Bank lassen zum verzinsen. | |
| q = | Zinsfaktor |
| Dies ist der Faktor der exponentiellen Zunahme des Kapitals. | |
Die Zinseszinsformel für variablen Zinssatz
| Die zuvor behandelte Zinseszinsformel gilt nur für den Fall, dass der Zinssatz über die gesamte Laufzeit der Kapitalanlage konstant bleibt. Nun gibt es aber auch Sparformen, bei denen je nach Anlagelänge des Kapitals ein stufenweise steigender Zinssatz gilt. Wir sprechen hier von Kapitalentwicklung mit variablem Zinssatz. In diesem Falle gilt die erweiterte Zinseszinsformel |
|
 |
|
Sei p1 % der gültige Zinssatz im ersten Jahr, so ist q1 mit  der Zinsfaktor für das erste Jahr; q2 mit  der Zinsfaktor für das zweite Jahr; q3 mit  der Zinsfaktor für das dritte Jahr; … usw. bis qn mit  der Zinsfaktor für das letzte Jahr der Anlage. |
|
Berechnungsmethoden
| Wollen wir von der Zinseszinsformel Kn=K0⋅qn bzw. Kn=K0⋅q1⋅q2⋅q3⋅…⋅qn eine der vier Variablen bzw. 2+n Variablen berechnen, so müssen uns stets die anderen Variablen in irgendeiner Form gegeben sein. Bei den Aufgabenstellungen handelt es sich zumeist um Textaufgaben. Wir müssen also zunächst durch Textinterpretation ermitteln, welche der Variablen gegeben ist und welche Variable gesucht wird. Je nachdem führt uns dies zu unterschiedlichen Berechnungsmethoden. |
Berechnung des Endkapitals
Zur Berechnung des Endkapitals müssen die Variablen K0, q bzw. q1, q2,… qn sowie n gegeben sein.Beispiel 1Lösung 1 |
Beispiel 2Lösung 2 |
Berechnung des Anfangskapitals
Zur Berechnung des Anfangskapitals müssen die Variablen Kn, q bzw. q1, q2,… qn sowie n gegeben sein.Beispiel 3Lösung 3 |
Beispiel 4Lösung 4 |
Berechnung des Zinssatzes
Zur Berechnung des Zinssatzes müssen die Variablen K0, Kn sowie n gegeben sein. Bei variablem Zinssatz müssen die Zinssätze bis auf einen einzigen ebenfalls gegeben sein.Beispiel 5Lösung 5 |
Beispiel 6Lösung 6 |
Berechnung des Anlagezeitraums
| Zur Berechnung des Anlagezeitraums müssen die Variablen Kn, K0 sowie q gegeben sein. Berechnungen von Anlagezeiträumen mit vareiablen Zinssätzen sind nicht möglich. Hinweis: Zur Berechnung des Anlagezeitraums sind Kenntnisse der Logarithmus-Rechnung erforderlich. Beispiel 7Lösung 7 |
Berechnung von Jahreszinsen
| Manchmal ist es von Interesse, wieviel Zinsen es in einem bestimmten Anlagejahr gab. Hierzu müssen - wie bei der Berechnung des Endkapitals - die Variablen K0, q bzw. q1, q2,… qn sowie n gegeben sein. Wird nun nach den erhaltenen Zinsen in einem bestimmten Jahr gefragt – z. B. im dritten Jahr – so berechnen wir dies über das Endkapital des dritten Jahres abzüglich des Endkapitals des 2. Jahres. Beispiel 8Lösung 8 |
Beispiel 9Lösung 9 |
Berechnung des Gesamtzinsertrages absolut und relativ
| Es ist auch von Interesse zu wissen, wieviel Zinsen insgesamt verdient wurden und zwar absolut als auch relativ. Den absoluten Zuwachs (in €) ermitteln wir aus Zges=Kn-K0. Den relativen Zuwachs (in %) ermitteln wir aus  .Beispiel 10Lösung 10Beispiel 11Lösung 11 |
Kapitalentwicklung Zinseszinsen fester Zinssatz Aufgabenblatt Level 1 / Blatt 1  42 Aufgaben im Blatt |
| Kapitalentwicklung Zinseszinsen variabler Zins Aufgabenblatt Level 1 / Blatt 2 49 Aufgaben im Blatt |
| Kapitalentwicklung Zinseszinsen fester Zinssatz Aufgabenblatt Level 1 / Blatt 3 43 Aufgaben im Blatt |
| Kapitalentwicklung Zinseszinsen fester Zins Aufgabenblatt Level 2 / Blatt 1 21 Aufgaben im Blatt |
| Kapitalentwicklung Zinseszinsen variabler Zins Aufgabenblatt Level 2 / Blatt 2 19 Aufgaben im Blatt |
| Kapitalentwicklung Zinseszinsen Aufgabenblatt Level 3 / Blatt 1 20 Aufgaben im Blatt |
| Kapitalentwicklung Zinseszinsen Aufgabenblatt Level 3 / Blatt 2 7 Aufgaben im Blatt |
