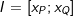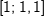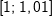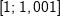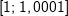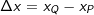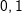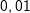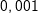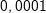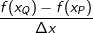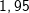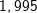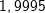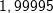 |
|
Momentane (lokale) Änderungsrate der Differenzialrechnung |
Momentane Änderungsrate Einleitung
| Haben wir im Kapitel „Mittlere Änderungsrate“ kennengelernt, wie wir das Steigungsverhalten von Kurven zwischen zwei bestimmten Kurvenpunkten ermitteln, so ist es auch von Interesse zu wissen, wie die Änderungsrate in einem einzigen bestimmten Punkt der Kurve aussieht. Um zu verdeutlichen, wie das geschieht, betrachten wir wieder das Beispiel mit dem schiefen Turm zu Pisa aus dem Kapitel „Mittlere Änderungsrate“. |
Regeln und Beispiele
| In nebenstehender Grafik sehen wir zunächst die Ausgangssituation. Die mittlere Änderungsrate zwischen den Punkten P und Q beträgt -9,81 m/s. Wir möchten wissen, welche Geschwindigkeit denn genau im Punkt Q herrscht. Hierzu lassen wir den Punkt P entlang der Kurve auf den Punkt Q zuwandern. |
Du kannst die Animation starten, indem du auf das  -Symbol (in der oberen Grafik unten links in der Ecke) klickst. Willst du die Animation anhalten, so klicke auf das  -Symbol (ebenfalls unten links in der Ecke).Beachte, wie sich die Koordinaten des Punktes P und auch der Differenzenquotient 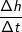 sich verändert.Hast du den Punkt P dann soweit verschoben, dass er mit dem Punkt Q zusammenfällt, zeigt uns der Differenzenquotient dann die genaue Geschwindigkeit im Punkt Q mit -18,57 m/s an. Dies führt uns zu folgendem Merksatz: |
Beispiel 1
Gegeben ist die Funktion f mit  . |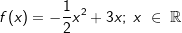
|
| a) | Berechne die mittlere Änderungsrate im Intervall I=[1;3]. |
| b) | Berechne die momentane Änderungsrate an der Stelle x=1. Interpretiere den Sachverhalt geometrisch. |
Lösung 1
| a) b) |
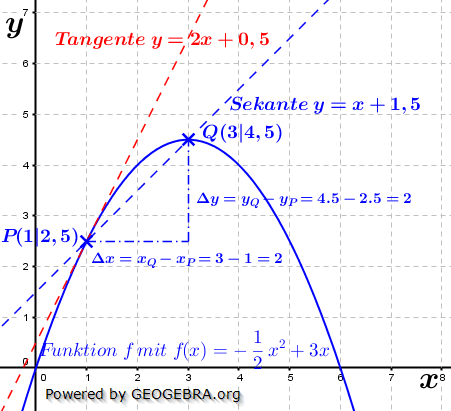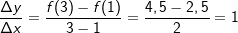 Mittlere Änderungsrate in I=[1;3]: Momentane Änderungsrate in x=1: Hierzu wählen wir den Punkt P(1|f(1)) und einen Punkt Q, der etwas weiter rechts von P zu liegen kommt, zum Beispiel den Punkt Q(1,1|f(1,1)). Mithilfe einer Tabelle berechnen wir nun mehrere Differenzenquotienten, indem wir die x–Koordinate von Q immer näher an die x-Koordinate von P heranrücken. Das sieht dann so aus: |
|||||||||||||||
|
||||||||||||||||
Je näher wir also dem Punkt kommen, umso näher kommt 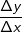 der Zahl 2.Wir können also sagen, dass die Steigung der Tangente an die Kurve im Punkt P(1|f(1)) mt=2 ist. Mathematisch ausgedrückt: Die mittlere Änderungsrate auf I=[1;xQ] strebt für Δx→0 gegen 2. Die momentane Änderungsrate in xP=1 ist 2. |
Geometrische Bedeutung
| Die momentane (lokale) Änderungsrate in xP=1 ist gleich der Steigung der Tangente durch den Punkt P(1|f(1)). Dies ist gleichzeitig die Steigung des Graphen der Funktion in xP=1. |
Beispiel 2
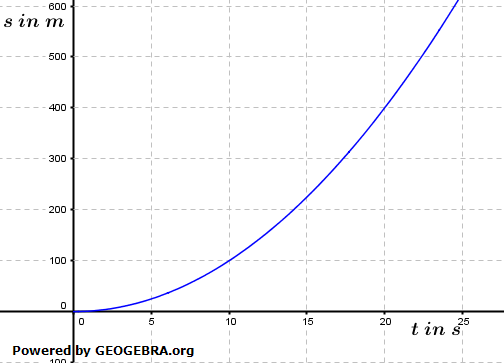  Ein Flugzeug beschleunigt beim Startvorgang bis zum Abheben.Das s-t-Diagramm zeigt den zurückgelegten Weg s in m in Abhängigkeit von der Zeit t in s. 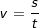 berechnen.Bestimme die Geschwindigkeit des Flugzeuges zum Zeitpunkt t=10 s aus dem Diagramm heraus. |
Lösung 2
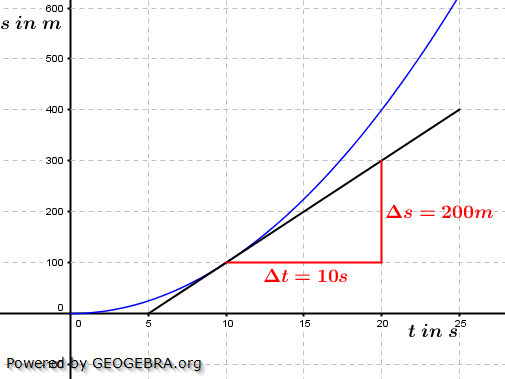 Da wir keine Messdaten zur Verfügung haben, sondern nur den Graphen im s-t-Diagramm, legen wir eine Tangente an den Graphen bei t=10 s. Wir tragen dann ein geeignetes Steigungsdreieck an die Tangente an und ermitteln daraus den Differenzenquotienten. Aus der Grafik lesen wir ab: 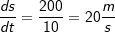 Die Geschwindigkeit des Flugzeuges zum Zeitpunkt t=10 s beträgt 20 m/s. |
Momentane Änderungsrate Aufgabenblatt Level 1 / Blatt 1  11 Aufgaben im Blatt |
| Momentane Änderungsrate Aufgabenblatt Level 1 / Blatt 2 14 Aufgaben im Blatt |
| Momentane Änderungsrate Aufgabenblatt Level 2 / Blatt 1 11 Aufgaben im Blatt |
| Momentane Änderungsrate Aufgabenblatt Level 2 / Blatt 2 14 Aufgaben im Blatt |
