 |
|
Vom Differenzenquotienten zur Ableitung in der Differenzialrechnung
|


Vom Differenzenquotienten zur Ableitung - Einleitung
| Im Kapitel „Momentane Änderungsrate“ haben wir gelernt, dass die momentane Änderungsrate der Steigung des Graphen einer Funktion in einem bestimmten Punkt entspricht, und gleich der Steigung der Tangente an den Graphen in diesem Punkt ist. Berechnet haben wir dort über eine umständliche Tabellenkalkulation. Nun fragen wir uns natürlich, ob dies auch effizienter über eine einfache Rechenoperation möglich ist. |
Regeln und Beispiele
| Dieses Kapitel bringt dir nun diese Rechenoperation näher. Wir unterscheiden dabei zwei wesentliche Operationen, nämlich |
Steigungsbestimmung in einem bestimmten Punkt
| Betrachten wir zunächst die Steigungsbestimmung in einem bestimmten Punkt. Der Mathematiker unterscheidet hier nach zwei Methoden, zum einen der sogenannten "x"–Methode und zum anderen der sogenannten "h"–Methode. |
Beispiel 1
| Bestimme für die Funktion f mit f(x)=x2-4x die Steigung im Punkt P(3|f(3)). |
Lösung 1 'x'-Methode
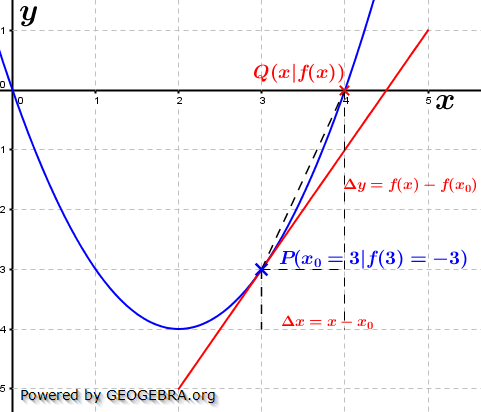 Auch hier müssen wir den Differenzenquotienten aufstellen. Ein beliebiger Punkt Q auf f hat die Koordinaten Q(x|f(x)). Auch hier müssen wir den Differenzenquotienten aufstellen. Ein beliebiger Punkt Q auf f hat die Koordinaten Q(x|f(x)).Wir bilden den Differenzenquotienten mit 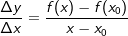 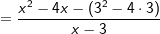 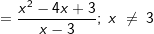 Der Zähler x2-4x+3 lässt sich faktorisieren zu (x-3)⋅(x-1), sodass gilt: 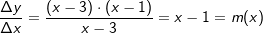 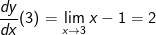 Die Steigung der Tangente an f in P(3|-3) und damit auch die Steigung der Kurve beträgt 2. Hinweis: Die "x"-Methode ist im gymnasialen Schulbetrieb unüblich, wird jedoch an Universitäten behandelt. |
Lösung 1 'h'-Methode
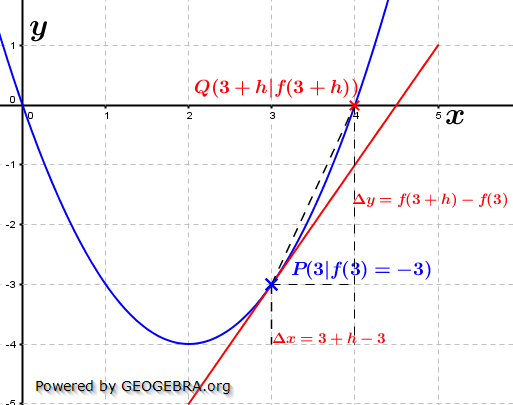 Im Gegensatz zur "x"-Methode wird hier ein beliebiger Abstand h der x-Koordinate, den der Punkt Q zu P hat, herangezogen (siehe Grafik). Im Gegensatz zur "x"-Methode wird hier ein beliebiger Abstand h der x-Koordinate, den der Punkt Q zu P hat, herangezogen (siehe Grafik).Die Aufstellung des Differenzenquotienten führt damit zu: 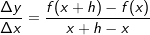 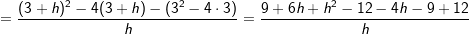 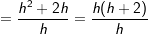 | mit h gekürzt | mit h gekürzt =h+2 Läuft nun h gegen Null, so bedeutet dies, dass der Punkt Q auf dem Graphen von f solange verschoben wird, bis Q mit P zusammenfällt. In diesem Falle wird dann aus der Sekante durch P und Q die Tangente in P. 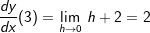 Die Steigung der Tangente an f in P(3|-3) und damit auch die Steigung der Kurve beträgt m3=2. |
Steigungsbestimmung in beliebigen Punkten
| Betrachten wir nun die Steigungsbestimmung in einem beliebigen Punkt. (auf die "x"–Methode wird hier nicht mehr näher eingegangen). Zunächst führen wir hier einen neuen Begriff ein, die „Ableitung“. Spricht der Mathematiker nämlich von der Steigungsbestimmung in einem beliebigen Punkt des Graphen einer Funktion , so sagt er hier kurz „Ableitung von f". Und selbstverständlich hat er sich auch ein diesbezügliches Formelzeichen ausgedacht, nämlich f' (sprich: f Strich). f' wiederum ist eine Abkürzung für den Differenzialquotienten 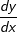 , der wiederum aus dem Differenzenquotienten , der wiederum aus dem Differenzenquotienten 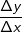 hervorgeht. hervorgeht.Der Differenzenquotient 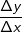 wird zum Differenzialquotienten wird zum Differenzialquotienten 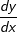 in dem Moment, wo die beiden Punkte P und Q zusammenfallen und aus der Sekante eine Tangente wird. in dem Moment, wo die beiden Punkte P und Q zusammenfallen und aus der Sekante eine Tangente wird. |
Beispiel 2
Gegeben ist die Funktion f mit 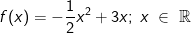 . .Bilde mit Hilfe der "h"–Methode die Ableitungsfunktion f'(x). |
Lösung 2
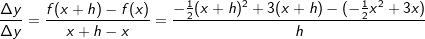 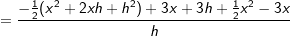 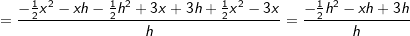 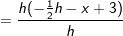 | h kürzen | h kürzen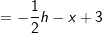 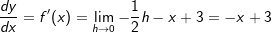 Die Funktionsgleichung der Ableitung von f in einem beliebigen Punkt P(x|f(x)) lautet f'(x)=-x+3. |
Weitere Beispiele
Beispiel 3
Gegeben ist die Funktion f mit 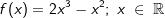 . .Bilde mit Hilfe der "h"–Methode die Ableitungsfunktion f'(x). |
Lösung 3
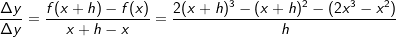 In dieser Lösungsformel befindet sich nun das (x+h)3. Die einfachste Form binomische Formeln mit einer Potenz größer als 2 aufzulösen ist über das Pascalsche Dreieck, weshalb wir es hier noch einmal behandeln.  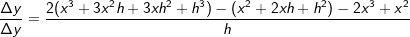 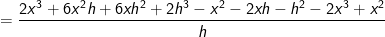 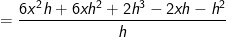 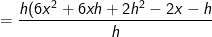 | | 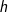 kürzen kürzen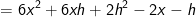 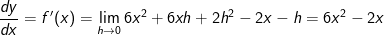 Die Funktionsgleichung der Ableitung von f in einem beliebigen Punkt P(x|f(x)) lautet f'(x)=6x2-2x. |
Beispiel 4
Gegeben ist die Funktion f mit 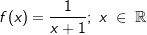 . .Bilde mit Hilfe der "h"–Methode die Ableitungsfunktion f'(x). |
Lösung 4
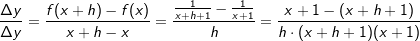 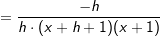 | | 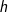 kürzen kürzen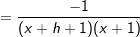 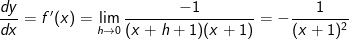 Die Funktionsgleichung der Ableitung von f in einem beliebigen Punkt P(x|f(x)) lautet 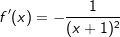 . . |
Beispiel 5
Gegeben ist die Funktion f mit 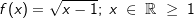 . .Bilde mit Hilfe der "h"–Methode die Ableitungsfunktion f'(x). |
Lösung 5
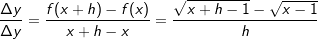 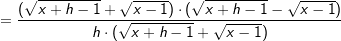 | erweitert mit | erweitert mit 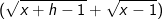 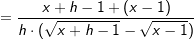 | Auflösung 3. binomische Formel | Auflösung 3. binomische Formel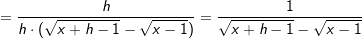 | |  kürzen kürzen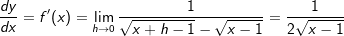 Die Funktionsgleichung der Ableitung von f in einem beliebigen Punkt P(x|f(x)) lautet 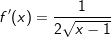 . . |
| Vom Differenzenquotienten zur Ableitung Aufgabenblatt Level 1 / Blatt 1 15 Aufgaben im Blatt |
| Vom Differenzenquotienten zur Ableitung Aufgabenblatt Level 1 / Blatt 2 17 Aufgaben im Blatt |
| Vom Differenzenquotienten zur Ableitung Aufgabenblatt Level 1 / Blatt 3 29 Aufgaben im Blatt |
| Vom Differenzenquotienten zur Ableitung Aufgabenblatt Level 2 / Blatt 1 17 Aufgaben im Blatt |
| Vom Differenzenquotienten zur Ableitung Aufgabenblatt Level 2 / Blatt 2 11 Aufgaben im Blatt |
| Vom Differenzenquotienten zur Ableitung Aufgabenblatt Level 2 / Blatt 3 21 Aufgaben im Blatt |
| Vom Differenzenquotienten zur Ableitung Aufgabenblatt Level 3 / Blatt 1 12 Aufgaben im Blatt |
| Vom Differenzenquotienten zur Ableitung Aufgabenblatt Level 3 / Blatt 2 16 Aufgaben im Blatt |
| Vom Differenzenquotienten zur Ableitung Aufgabenblatt Level 4 / Blatt 1 4 Aufgaben im Blatt |



