 |
Differenzialrechnung - Die mittlere Änderungsrate |
Mittlere Änderungsrate Einleitung
| In der Regel laufen dynamische Vorgänge nicht konstant (gleichmäßig) ab, sondern unterliegen im Verlaufe des Vorgangs unterschiedlichen Schwankungen. So ändert sich die Bevölkerungszahl eines Landes, der Durchmesser eines Baumes, die Anzahl der Bakterien, die Geschwindigkeit eines Autos, der Zufluss in ein Gefäß usw. nicht konstant, sondern sind auf die Zeitachse bezogen, unterschiedlichen Zunahmen der Bestandsgrößen unterzogen. Bei solchen Vorgängen kommt es jedoch nicht nur auf den aktuellen Bestand an, sondern auch darauf, wie schnell sich die Bestandsgröße ändert. Diese „Schnelligkeit“ versuchen wir, mathematisch zu beschreiben. Um zu lernen, wie du zur mittleren Änderungsrate kommst, kannst du dir die nachfolgenden Videos ansehen, oder aber du liest dir die verbalen Beschreibungen im Einzelnen durch. |
Video zur mittleren Änderungsrate (Laufzeit ca. 6 Minuten)
Regeln und Beispiele
Aufgabe 1
Während eines Dauerregens wird die Wassermenge V (in Liter) in einer Regentonne in Abhängigkeit von der Zeit t (in Minuten) gemessen.
|
 |
Lösung 1
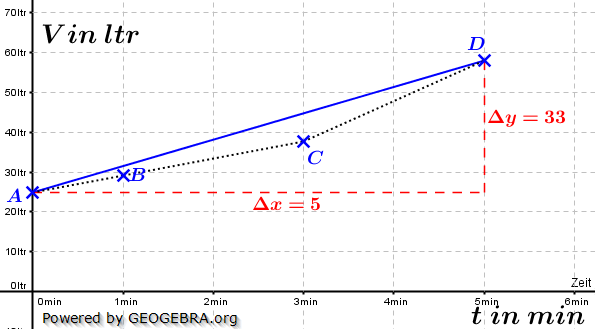 Der Eintrag der Messpunkte in ein Koordinatensystem führt zum Schaubild gemäß nebenstehender Grafik. Wie du siehst, läuft der Vorgang nicht kontinuierlich ab (beachte die gepunkteten Linien).Die blaue Linie stellt nun die mittlere Änderungsrate in den ersten 5 Minuten dar. Diese Linie ist Teil einer Geraden durch die beiden Punkte A und D. Bekanntlich haben Geraden ja eine Steigung m. Der Wert dieser Steigung ist gleich dem Wert der mittleren Änderungsrate in den ersten 5 Minuten. In der Mittelstufe haben wir die Steigung einer Geraden mithilfe der Formel 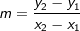 berechnet. Diese Berechnung gilt auch für die mittlere Änderungsrate, nur dass wir jetzt an Stelle von m schreiben 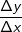 . Um den Bereich zu beschreiben, für den wir die mittlere Änderungsrate bestimmen wollen, schreiben wir I=[a;b] (gesprochen „Im Intervall von a bis b“). In unserem Beispiel ist a=0 und b=5. Mithilfe dieser Definitionen können wir nun die mittlere Änderungsrate (die ja eine Änderungsrate des Volumens ist) berechnen mit: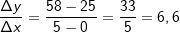 Die mittlere Volumenänderung in I=[0;5] beträgt 6,6 ltr/min. Der mathematische Namen für 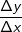lautet „Differenzenquotient“. |
Aufgabe 2
| Berechne mithilfe des Differenzenquotienten die mittlere Volumenänderung der Messwerte aus Beispiel 1 in den Intervallen I=[0;1], I=[1;3] und I=[1;5]. |
Lösung 2
   |
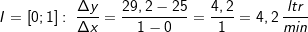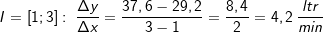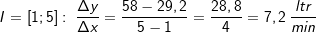Geometrische Bedeutung
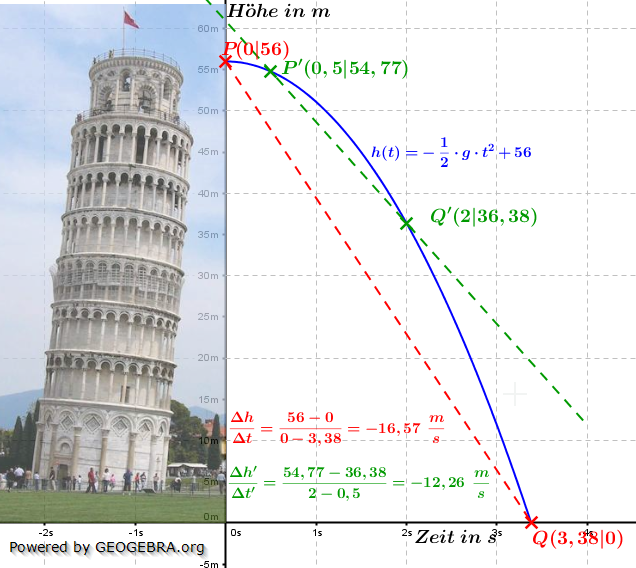 Wie wir in den beiden Beispielen gesehen haben, verändert sich die mittlere Änderungsrate je nachdem, zwischen welchen Messpunkten wir sie berechnen. Nun lassen sich solche Messreihen auch durch mathematische Funktionen beschreiben, denen eine Funktions-gleichung zugrunde liegt.Betrachten wir uns einmal die h-t–Funktion des freien Falls. Ihre Funktionsgleichung lautet ja 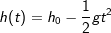 mit g=9,81 m/s2 als Erdbeschleunigung (Ortsfaktor). Wir lassen einen Stein vom schiefen Turm in Pisa aus rund h0=56 m Höhe herunterfallen. Der Graph der Funktion des freien Falls ist ja eine Parabel wie obenstehend abgebildet. Die Fallgeschwindigkeit des Steins wird ja stets größer, bis er auf der Erde aufschlägt. Nun wollen wissen, mit welcher Durchschnittsgeschwindigkeit der Stein fällt, bilden also den Differenzenquotienten zwischen den Punkten P und Q, also in I=[0;3,38]. Die Berechnung zeigt, dass wir eine mittlere Fallgeschwindigkeit von 16,57 m/s haben. Bei der Fallstrecke zwischen den Punkten P' und Q', also in I=[0,5;2], kommen wir zu einer mittleren Fallgeschwindigkeit von 12,26 m/s. (Dass die Geschwindigkeiten in der Grafik mit „-„ angegeben sind, rührt daher, dass der Stein ja nach unten fällt.) Betrachten wir uns noch einmal die obige Grafik. Die rote Linie für I=[0;3,38] schneidet ja den Graphen der h-t–Funktion in den Punkten P und Q. Sie ist also, bezüglich des Graphen eine Sekante. Gleiches gilt auch für die grüne Linie mit den Punkten P' und Q', sie ist ebenfalls eine Sekante. Sekanten sind im mathematischen Sinne Geraden und über den Differenzenquotienten haben wir die Steigung dieser Geraden berechnet. Mit anderen Worten: |
{snippet snippet-aufgabenblatt-level}
Mittlere Änderungsrate Aufgabenblatt Level 1 / Blatt 1  9 Aufgaben im Blatt |
| Mittlere Änderungsrate Aufgabenblatt Level 1 / Blatt 2 11 Aufgaben im Blatt |
| Mittlere Änderungsrate Aufgabenblatt Level 1 / Blatt 3 16 Aufgaben im Blatt |
| Mittlere Änderungsrate Aufgabenblatt Level 2 / Blatt 1 10 Aufgaben im Blatt |
| Mittlere Änderungsrate Aufgabenblatt Level 2 / Blatt 2 6 Aufgaben im Blatt |
| Mittlere Änderungsrate Aufgabenblatt Level 3 / Blatt 1 16 Aufgaben im Blatt |
| Mittlere Änderungsrate Aufgabenblatt Level 3 / Blatt 2 15 Aufgaben im Blatt |
